
Ответы на курс: Основы теории информации и криптографии
Древовидные коды также называют:
|
параллельными кодами |
 |
последовательными кодами |
|
управляющими кодами |
Преимущество матричного кодирования заключается в:
|
определении объема полученных данных еще до начала кодирования |
 |
использовании гораздо меньшего объема памяти по сравнению с другими методами кодирования |
|
использовании большего объема памяти по сравнению с другими методами кодирования |
Коды с исправлением ошибок предназначены для:
|
управления ошибками в ходе отправки и получения сообщения |
 |
восстановления с вероятностью, близкой к единице, посланного сообщения |
|
выявления вероятности, близкой к единице, наличие ошибок |
Код Хэмминга:
|
не групповой код |
|
натуральный код |
 |
групповой код |
Для кодирующей матрицы  найти вероятность правильной передачи:
найти вероятность правильной передачи:
 |
Pправильной передачи = p4+p3q |
|
Pправильной передачи = p2+p2q |
|
Pправильной передачи = p3+p2q |
Блочный код называется групповым, если:
|
сообщение кодируется несколькими методами последовательно |
|
он образует группу вместе с другими кодами |
 |
его кодовые слова образуют группу |
Для кодирующей матрицы 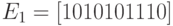 найти вероятность необнаружения ошибки:
найти вероятность необнаружения ошибки:
|
Pнеобнаружения ошибки = 2p3q3 + pq3 |
 |
Pнеобнаружения ошибки = 2p2q3 + pq4 |
|
Pнеобнаружения ошибки = 4p4q3 + pq4 |
Построить CRC-4 код для сообщения 10000000, используя полином-генератор x4+1:
|
1101 |
|
1001 |
 |
1000 |
Первый БЧХ-код, примененный на практике, был:
 |
(92,127)-код |
|
(102,250)-код |
|
(231,255)-код |
Код Голея — это:
|
код БЧХ |
|
невозможно определить принадлежность кода Голея к коду БЧХ |
 |
не код БЧХ |
При реальной передаче или хранении информации ошибки:
|
распределяются равномерно по всей длине данных |
|
группируются в нескольких участках, распределенных неравномерно |
 |
обычно группируются на некотором участке |
Первая и наиболее известная система с открытым ключом называется:
|
DES |
|
PGP |
 |
RSA |
Особенностью системы с ключевым словом является:
|
три уровня секретности |
|
один уровень секретности |
 |
два уровня секретности |
Нужно послать секретные сообщения 25 и 2 для JB и 14 для CIA, используя следующие записи открытой книги паролей криптосистемы RSA — JB: 77,7; CIA: 667,15
|
43, 41; 256 |
|
53, 31; 295 |
 |
53, 51; 247 |
Системы с ключевым словом характеризуются тем, что:
 |
широко применяются до сих пор |
|
в настоящее время очень редко применяются |
|
вышли из применения |
Большинство тегов языка HTML:
|
самодостаточные |
|
нуждаются в двойном закрытии |
 |
парные |
Самым распространенным типом данных в компьютерном мире является:
|
графические файлы |
|
динамические библиотеки |
 |
текстовые файлы |
Аналоговая информация характеризуется:
 |
непрерывным процессом изменения некоторой величины |
|
последовательными точными значениями некоторой величины |
|
повторными процессами распределения случайной величины |
Кибернетика — это наука:
|
о способах взаимодействиях различных абстрактных объектов |
|
об общих законах управления системами |
 |
об общих законах получения, хранения, передачи и переработки информации |
Чем ниже частота дискретизации, тем:
|
точнее происходит перевод непрерывной информации в дискретную |
|
эффективнее и быстрее происходит перевод непрерывной информации в дискретную |
 |
менее точно происходит перевод непрерывной информации в дискретную |
В таблице кодировки ASCII+ печатные и управляющие символы занимают:
|
все 256 символов таблицы |
|
первые 127 позиций таблицы |
|
последние 127 позиций таблицы |
|
последние 128 позиций таблицы |
 |
первые 128 позиций таблицы |
Дискретные случайные величины X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Вычислить HX1.
|
HX1 = 1.51 \ бит/сим |
 |
HX1 = 2 \ бит/сим |
|
HX1 = 2.5 \ бит/сим |
Определить HZ, если задана дискретная случайная величина Z=(X1+1)2-X2, где независимые дискретные случайные величины X1, X2 могут с равной вероятностью принимать значение либо 0, либо 1:
|
HZ = 1 бит/сим |
 |
HZ = 2 бит/сим |
|
HZ = 2.5 бит/сим |
Дискретная случайная величина X равна количеству «гербов», выпавших на двух идеальных монетках. Найти энтропию X:
|
HX=1.8 бит/сим |
|
HX=2.5 бит/сим |
 |
HX=1.5 бит/сим |
По теории Шеннона:
 |
смысл сообщений НЕ имеет никакого отношения к теории информации |
|
нельзя дать точный ответ насчет зависимости между смыслом сообщений и теории информации |
|
смысл сообщений имеет прямое отношения к теории информации |
Перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия испытаний, в которых каждая лампочка зажигается с определенной вероятностью pi, где i — это номер лампочки. Среднее время, необходимое для правильного ответа испытуемого, пропорционально:
 |
величине энтропии  |
|
 |
|
числу лампочек N |
Про дискретную случайную величину X известно, что ее значениями являются буквы кириллицы. Произведен ряд последовательных измерений X, результат которых — «ТЕОРИЯИНФОРМАЦИИ». Составить на основании этого результата приблизительный закон распределения вероятностей этой дискретной случайной величины и оценить минимальную среднюю длину кодов для X:
 Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока — 2 бита:
Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока — 2 бита:
|
1.7 бит/сим |
|
1.3 бит/сим |
 |
1.56 бит/сим |
Метод Шеннона-Фэно состоит в том, что:
|
значения дискретной случайной величины располагают в порядке возрастания их вероятностей, а затем последовательно умножают на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй — 1 |
 |
значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй — 1 |
|
значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 1, а к коду второй — 0 |
Среднее количество бит, приходящихся на одно кодируемое значение дискретной случайной величины:
 |
не может быть меньшим, чем энтропия этой дискретной случайной величины |
|
не может быть большей, чем энтропия этой дискретной случайной величины |
|
строго равна энтропии этой дискретной случайной величины |
Суть основной теоремы о кодировании при отсутствии помех заключается в том, что:
|
при очень малой длине n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения. Данное правило действует только на короткие сообщения |
 |
с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения |
|
с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет очень удалено от энтропии единицы сообщения |
Размер сжатия:
|
может быть сколь угодно большим |
 |
не может быть больше некоторого теоретические предела |
|
ограничивается лишь потребностями пользователя |
Вычислить HX для кодов Хаффмена и Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей  :
:
Вычислить ML(X) для кода Шеннона-Фэно для X. Дискретная случайная величина X задается следующим распределением вероятностей  :
:
Вместе с собственно сообщением нужно передавать таблицу кодов для метода:
|
Берга |
 |
Шеннона-Фэно |
|
Винера |
 |
Хаффмена |
Преимущество арифметического кодирования позволяет:
|
кодировать символы одним байтом |
 |
кодировать некоторые символы менее чем одним битом |
|
кодировать некоторые символы только несколькими битами |
Закодировать сообщение «КИБЕРНЕТИКИ», используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
 |
код(КИБЕРНЕТИКИ) = ‘К’0′И’00′Б’100′Е’000′Р’1 100′Н’1111000′Т’100110111 |
|
код(КИБЕРНЕТИКИ) = ‘К’0′И’00′Б’101′Е’010′Р’1 100′Н’1100001′Т’100110001 |
|
код(КИБЕРНЕТИКИ) = ‘К’0′И’00′Б’100′Е’000′Р’1 100′Н’1111000′Т’101010001 |
Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длины кодов Хаффмена, блочного Хаффмена (для блоков длины 2 и 3) для сообщения ABAAAB:
|
LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 6 бит, LХаффмена-3(ABAAAB) = 4 бита |
 |
LХаффмена-1(ABAAAB) = 6 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 5 бит |
|
LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 6 бит |
Cообщение, полученное путем сжатия адаптивным алгоритмом Хаффмена с упорядоченным деревом имеет вид: ‘A’0′F’00′X’0111110101011011110100101. Определить длину несжатого сообщения в битах:
|
117 бит |
 |
120 бит |
|
125 бит |
Составить арифметический код для сообщения BAABC, полученного от дискретной случайной величины X со следующим распределением вероятностей P(X=A)=1/3, P(X=B)=7/15, P(X=C)=1/5:
|
01100001 |
|
01100111 |
 |
01011111 |
Дискретная случайная величина X может принимать три различных значения. Если считать сложность построения кода пропорциональной количеству различных значений кодируемой дискретной случайной величины, то блочный код для X по сравнению с неблочным сложнее строить в:
|
в 81 раз |
|
в 25 раз |
 |
в 27 раз |
Закодировать сообщение «AABCDAACCCCDBB», используя адаптивный алгоритм Хаффмена с упорядоченным деревом:
|
код(AABCDAACCCCDBB) = ‘A’10′B’00′C’011′D’00011001111100110011110 |
 |
код(AABCDAACCCCDBB) = ‘A’10′B’00′C’000′D’00011001111100110011001 |
|
код(AABCDAACCCCDBB) = ‘A’11′B’11′C’010′D’00011001111100110000101 |
Словарные алгоритмы преимущественно отличаются от статистических тем, что:
|
позволяют кодировать последовательности символов одинаковой длины |
|
позволяют быстрее кодировать символы |
 |
позволяют кодировать последовательности символов разной длины |
Закодировать сообщения «КИБЕРНЕТИКИ», вычислить длины в битах полученных кодов, используя алгоритм LZSS (словарь — 12 байт, буфер — 4 байта):
|
 длина 10 * 9 = 90 бит длина 10 * 9 = 90 бит |
 |
 длина 3 * 7 + 7 * 9 = 84 бит длина 3 * 7 + 7 * 9 = 84 бит |
|
 длина 3 * 7 + 7 * 9 = 84 бит длина 3 * 7 + 7 * 9 = 84 бит |
Алгоритм LZ77 использует «скользящее» по сообщению окно, разделенное на две части, выполняющие определенные функции:
 |
первая, большая по размеру, включает уже просмотренную часть сообщения. Вторая, намного меньшая, является буфером, содержащим еще незакодированные символы входного потока |
|
первая, большая по размеру, включает уже просмотренную часть сообщения. Вторая, намного меньшая, является буфером, содержащим уже закодированные, но еще не просмотренные символы входного потока |
|
первая включает уже просмотренную часть сообщения. Вторая является буфером, содержащим еще незакодированные символы входного потока. Первая и вторая части равны |
Статистическими методами называют:
|
словарные алгоритмы |
 |
арифметическое кодирование |
|
алгоритм Ферма |
 |
метод Хаффмена |
 |
метод Шеннона-Фэно |
Закодировать сообщения «AABCDAACCCCDBB», вычислить длины в битах полученных кодов, используя алгоритм LZ77 (словарь — 12 байт, буфер — 4 байта):
 |
 длина 8 * 15 = 120 бит длина 8 * 15 = 120 бит |
|
 длина 8 * 13 = 104 бита длина 8 * 13 = 104 бита |
|
 длина 8 * 10 = 80 бит длина 8 * 10 = 80 бит |
Алгоритм LZSS отличается от LZ77 следующим:
|
возможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря |
|
скоростью работы |
|
длина подстроки, которую можно закодировать, НЕ ограничена размером буфера |
 |
производимыми кодами |
Задержка сигнала во времени представляет собой:
 |
интервал времени от отправки сигнала передатчиком до его приема приемником |
|
интервал времени от создания сигнала до его прочтения приемником и удаления |
|
интервал времени от отправки сигнала передатчиком до его приема приемником и обратной отправки к передатчику |
Видеоинформацию можно сжать:
|
очень неплотно, всего на несколько процентов |
|
очень слабо — она практически не сжимаема |
 |
очень плотно, до 100 и более раз |
|
до 10000 и более раз |
Устройства канала связи представляют собой:
|
совокупность устройств, объединенных линиями связи, предназначенных для передачи информации от источника информации до ее приемника |
 |
устройства, просто передающие усиленным принятый сигнал |
|
устройство, определяющее интервал времени от отправки сигнала передатчиком до его приема приемником |
Cжатие с потерями позволяет:
|
предоставить более эффективные методы сжатия данных без удаления информации |
|
добавлять некоторую часть к исходной информации |
 |
отбрасывать часть исходной информации |
Для сжатия графической информации с потерями в конце 80-х установлен стандарт:
|
GIF |
|
ICO |
|
WMF |
|
BMP |
 |
JPEG |
Сжатие с потерями используется в основном для видов данных:
|
текстовая информация |
 |
звук |
 |
полноцветная графика |
 |
видеоинформация |
Специальные таблицы для перевода неформальных данных в цифровой вид называются:
|
символьные преобразователями |
|
таблицами взаимодействия |
|
таблицами шифрования |
 |
таблицами кодировки |
Противоположность информации:
 |
неопределенность |
|
определенность |
|
сущность |
Функция f-инъекция, если:
|
она зависит от двух и более аргументов |
 |
на разных значениях аргумента она принимает разные значения |
|
на разных значениях аргумента она принимает одинаковые значения |
|
в роли аргумента выступает функция |
Дискретная случайная величина X может принимать три различных значения. При построении блочного кода с длиной блока 4 для X необходимо будет рассмотреть дискретную случайную величину X — выборку четырех значений X. X может иметь:
|
75 различных значений |
 |
81 различное значение |
|
27 различных значений |
Вычислить длины в битах сообщения «СИНЯЯ СИНЕВА СИНИ» в коде ASCII+ и его полученного кода
|
L(СИНЯЯ СИНЕВА СИНИ) = 124 бит, длина исходного сообщения = 148 бит |
 |
L(СИНЯЯ СИНЕВА СИНИ) = 114 бит, длина исходного сообщения = 136 бит |
|
L(СИНЯЯ СИНЕВА СИНИ) = 104 бит, длина исходного сообщения = 124 бит |
Атрибут ALT тега IMG используется для:
|
указания способа выравнивания картинки |
|
указания URI файла с графикой |
 |
указания альтернативного текста, показываемого вместо картинки, в случае, когда файл с графикой недоступен или его тип неизвестен браузеру |
|
определения рамки картинки |
Составить адаптивный арифметический код с маркером конца для сообщения BAABC:
 |
01000010111001 |
|
01000010110100 |
|
01000011000011 |
Наиболее широкое распространение получил:
|
(102,250)-код |
 |
(231,255)-код |
|
(92,127)-код |

 найти вероятность правильной передачи:
найти вероятность правильной передачи: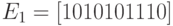 найти вероятность необнаружения ошибки:
найти вероятность необнаружения ошибки:



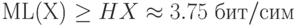
 Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока — 2 бита:
Вычислить ML1(X) для блочного кода Хаффмена для X. Длина блока — 2 бита: :
:


 :
: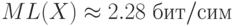
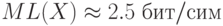

 длина 10 * 9 = 90 бит
длина 10 * 9 = 90 бит длина 3 * 7 + 7 * 9 = 84 бит
длина 3 * 7 + 7 * 9 = 84 бит длина 3 * 7 + 7 * 9 = 84 бит
длина 3 * 7 + 7 * 9 = 84 бит длина 8 * 15 = 120 бит
длина 8 * 15 = 120 бит длина 8 * 13 = 104 бита
длина 8 * 13 = 104 бита длина 8 * 10 = 80 бит
длина 8 * 10 = 80 бит
