 называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве  , если
, еслиОтветы на курс: Математический анализ
 называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве  , если
, если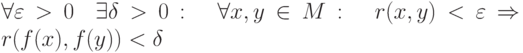 |
|
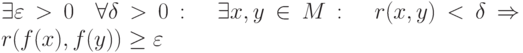 |
|
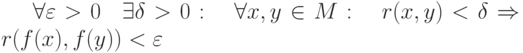 |
|
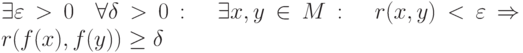 |
 является точкой локального максимума функции
является точкой локального максимума функции  , если
, если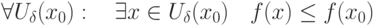 |
|
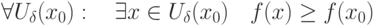 |
|
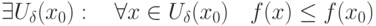 |
|
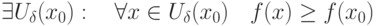 |
 является точкой локального минимума функции
является точкой локального минимума функции  , если
, если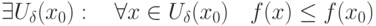 |
|
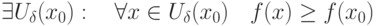 |
|
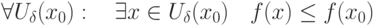 |
|
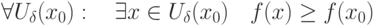 |
 для функции
для функции  является точкой разрыва
является точкой разрыва| устранимой | |
| второго рода | |
| с конечным скачком |
 существует и равен
существует и равен |
|
 |
|
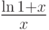 |
|
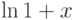 |
 в данной точке
в данной точке  называется
называется |
|
 |
|
 |
|
 |
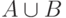 ,
,  если
если 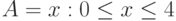 ,
, 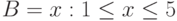 , если
, если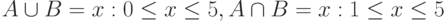 |
|
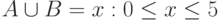 , , 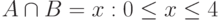 |
|
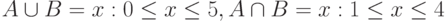 |
 , то
, то не является элементом множества не является элементом множества  |
|
 - элемент множества - элемент множества  |
|
 является подмножеством множества является подмножеством множества  |
|
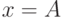 |
 элементов
элементов| 2n | |
| 2n | |
| 1 | |
| n2 |
 в в виде
в в виде  , если
, если  и
и  - натуральные числа, не имеющие общих делителей.
- натуральные числа, не имеющие общих делителей.| 1/18 | |
| 1/6 | |
| 13/18 | |
| 29/22 |
| всякая система вложенных отрезков имеет непустое пересечение, то есть существует по крайней мере одно число, которое принадлежит всем отрезкам данной системы | |
| у всякого числового множества верхняя (нижняя) грань единственна | |
| для каждого сечения множества действительных чисел существует число, производящее это сечение |
 - точка локального экстремума дифференцируемой функции
- точка локального экстремума дифференцируемой функции  . Тогда
. Тогда |
|
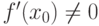 |
|
 |
 является пределом
является пределом  числовой функции
числовой функции  . Какие утверждения верны:
. Какие утверждения верны: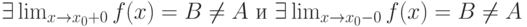 |
|
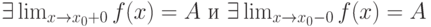 |
|
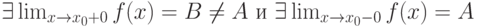 |
|
 |
 существует и равен
существует и равен |
|
 |
|
 |
|
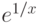 |
 - точка локального экстремума функции
- точка локального экстремума функции  . Тогда производная
. Тогда производная |
|
 или не существует или не существует |
|
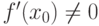 |
|
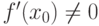 или не существует или не существует |
|
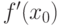 не существует не существует |
![f(x)=x-[x],\quad 0\leq x\leq 1](http://www.intuit.ru/sites/default/files/tex_cache/3d73868a6fa1fc5f680c1edf55a2cdc7.png) , где
, где ![[x]](http://www.intuit.ru/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) - означает целую часть от числа:
- означает целую часть от числа:непрерывность на ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) |
|
| f(a)=f(b) | |
дифференцируемость на  |
 функции
функции  :
: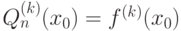 |
|
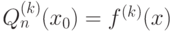 |
|
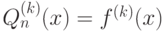 |
|
 |
 называется дифференцируемой в точке
называется дифференцируемой в точке  , если
, если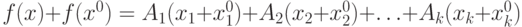 |
|
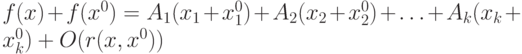 |
|
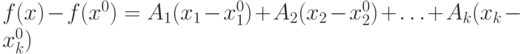 |
|
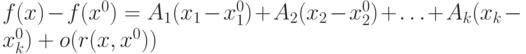 |

принадлежит интервалу  |
|
лежит вне отрезка ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) |
|
совпадает с концами отрезка  или или  |
|
| хотя бы одна | |
| единственная |
 непрерывна на
непрерывна на ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) и дифференцируема на
и дифференцируема на  . Какое утверждение верно:
. Какое утверждение верно:если  , то , то  локально возрастает локально возрастает |
|
если  возрастает на возрастает на ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то , то 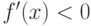 на на  |
|
если  возрастает на возрастает на ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то , то 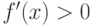 на на  |
|
если 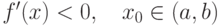 , то , то  локально возрастает локально возрастает |
|
если 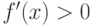 на на  , то , то  возрастает на возрастает на ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) |
 . Какие утверждения верны:
. Какие утверждения верны: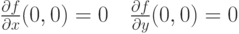 |
|
непрерывна на 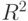 |
|
 дифференцируема в дифференцируема в 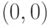 |
|
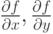 непрерывны в непрерывны в 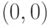 |
 для
для  раз дифференцируемой в окрестности точки
раз дифференцируемой в окрестности точки  функции
функции 
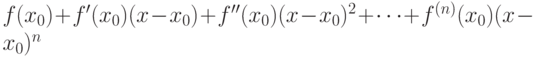 |
|
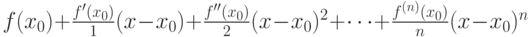 |
|
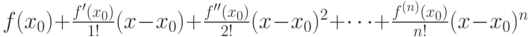 |
|
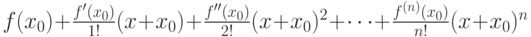 |
 в точке
в точке  :
: непрерывна в точке непрерывна в точке  |
|
Частные производные в точке  по каждому аргументу существуют и непрерывны в точке по каждому аргументу существуют и непрерывны в точке  |
|
существуют частные производные в точке  по каждому аргументу по каждому аргументу |
 называется возрастающей на
называется возрастающей на 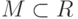 , если
, если 
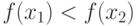 |
|
 |
|
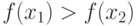 |
|
 |
![f(x,y)=\sqrt[3]{xy})](http://www.intuit.ru/sites/default/files/tex_cache/125cd39a13dce6a856a78e2f6d67fee1.png) . Какие утверждения верны:
. Какие утверждения верны: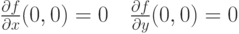 |
|
 дифференцируема в дифференцируема в 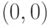 |
|
непрерывна на 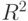 |
|
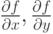 непрерывны в непрерывны в 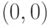 |
 . Какие утверждения верны:
. Какие утверждения верны:существуют 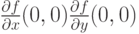 |
|
 дифференцируема в дифференцируема в 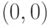 |
|
непрерывна на 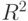 |
|
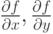 непрерывны в непрерывны в 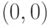 |
 .Какие утверждения верны:
.Какие утверждения верны:если 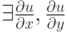 в точке в точке 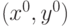 , то , то  дифференцируема в дифференцируема в 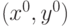 |
|
если  дифференцируема в дифференцируема в 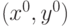 , то , то 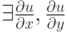 в точке в точке 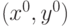 |
|
если 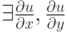 в данной точке в данной точке 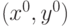 , то , то  непрерывна в непрерывна в 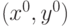 |
|
если  дифференцируема в дифференцируема в 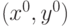 , то она непрерывна в , то она непрерывна в 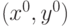 |
 . На каких множествах существует неявная функция
. На каких множествах существует неявная функция 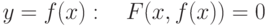 :
: |
|
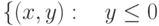 |
|
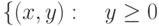 |
|
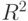 |
|
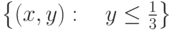 |
|
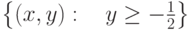 |
 . Тогда
. Тогда  равен
равен![[y\cos xy, \cos xy]](http://www.intuit.ru/sites/default/files/tex_cache/8a555d65acf5a400c7620675f3fce36d.png) |
|
![[\cos xy, x\cos xy]](http://www.intuit.ru/sites/default/files/tex_cache/d75894b8e21cc8606e614cdabedfabfc.png) |
|
![[y\cos xy, x\cos xy]](http://www.intuit.ru/sites/default/files/tex_cache/e17cd1d8e1516962d3df9edd729f8ef8.png) |
|
![[cos xy, cos xy]](http://www.intuit.ru/sites/default/files/tex_cache/6dbf849fde3f9b54c610bcf5fcaf1e0f.png) |
 в точке
в точке  и найти его модуль (длину):
и найти его модуль (длину):![\text{grad }f=[0,0,0]\quad |\text{grad }f|=0](http://www.intuit.ru/sites/default/files/tex_cache/7f35011419341a793303f8c81b68050d.png) |
|
![\text{grad }f=[2,2,2]\quad |\text{grad }f|=2\sqrt{3}](http://www.intuit.ru/sites/default/files/tex_cache/0fd91145c99f305fd7fda62fb915e460.png) |
|
![\text{grad }f=[1,1,1]\quad |\text{grad }f|=\sqrt{3}](http://www.intuit.ru/sites/default/files/tex_cache/a0ad8c9f54d646762bcf74bfda6298f5.png) |
 . Тогда частные производные 2 порядка равны:
. Тогда частные производные 2 порядка равны: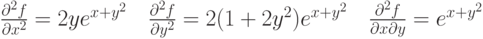 |
|
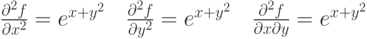 |
|
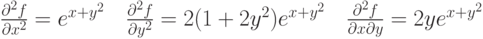 |
 точка экстремума функции
точка экстремума функции  при условии
при условии 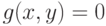 . Тогда линия уровня
. Тогда линия уровня 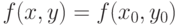 пересекает кривую
пересекает кривую  под углом
под углом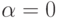 |
|
 |
|
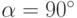 |
 равна:
равна: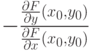 |
|
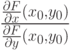 |
|
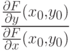 |
|
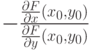 |
 является точкой локального максимума для функции
является точкой локального максимума для функции  , если существует окрестность
, если существует окрестность  :
: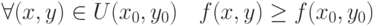 |
|
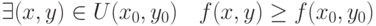 |
|
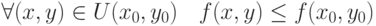 |
|
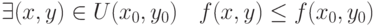 |
 , то
, то - элемент множества - элемент множества  |
|
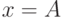 |
|
 является подмножеством множества является подмножеством множества  |
|
 не является элементом множества не является элементом множества  |

| пересечение множеств | |
| разность множеств | |
| объединение множеств | |
| симметрическая разность |
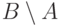 , если
, если  ,
, 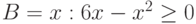
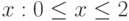 |
|
 |
|
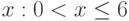 |
| 10 | |
| 4 | |
| 8 | |
| 16 |
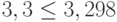 |
|
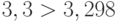 |
|
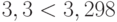 |
|
 |
| Y | |
| Q | |
| Z | |
| R |
| множество, ограниченное сверху | |
| множество, ограниченное снизу | |
| пустое множество | |
| множество, ограниченное и сверху, и снизу |
| n / m | |
| nm | |
| m / n | |
| mn |
![M = [a,b]](http://www.intuit.ru/sites/default/files/tex_cache/ddbb2a46ecbb84583c79a3d672aefcc2.png) , то
, то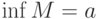 , , 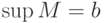 |
|
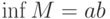 , , 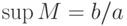 |
|
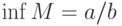 , , 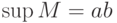 |
|
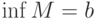 , , 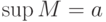 |
 в виде
в виде  , если
, если  и
и  - натуральные числа, не имеющие общих делителей.
- натуральные числа, не имеющие общих делителей.| 353/495 | |
| 13/2 | |
| 2/13 | |
| 211/99 |

| разность множеств | |
| объединение множеств | |
| симметрическая разность | |
| пересечение множеств |
 открытого шара
открытого шара  является множество
является множество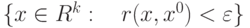 |
|
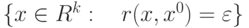 |
|
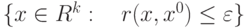 |
 - изолированная точка множества
- изолированная точка множества  . Какие утверждения верны:
. Какие утверждения верны: замкнутое замкнутое |
|
 содержит граничные точки содержит граничные точки |
|
 |
|
 предельная точка множества предельная точка множества  |
|
 не открытое множество не открытое множество |
|
 открытое множество открытое множество |
 в
в  вычисляется по формуле
вычисляется по формуле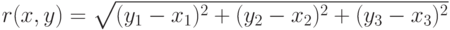 |
|
 |
|
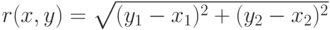 |
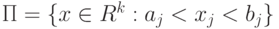 называется
называется| замкнутым параллелепипедом | |
замкнутым шаром радиуса  |
|
| открытым параллелепипедом | |
открытым шаром радиуса  |
 называется компактным, если оно
называется компактным, если оно| ограничено и замкнуто | |
| ограничено и содержит все свои предельные точки | |
| ограничено и содержит все свои граничные точки | |
| ограничено и открыто |
![G=(1,2)\cup\{3\}\cup(4,5]](http://www.intuit.ru/sites/default/files/tex_cache/28fd252433ae7c4b811044d1d69ce531.png) . Какое множество является множеством граничных точек
. Какое множество является множеством граничных точек  :
: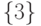 |
|
![[1,2]\cup[4,5]](http://www.intuit.ru/sites/default/files/tex_cache/bc4698707c4c7346f617b79354136479.png) |
|
 |
|
 |
 точки
точки  называется
называетсяоткрытый шар радиуса  с центром в точке с центром в точке  |
|
замкнутый шар радиуса  с центром в точке с центром в точке  |
 открытого шара
открытого шара  является множество
является множество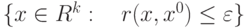 |
|
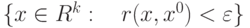 |
|
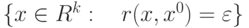 |
 называется граничной точкой множества
называется граничной точкой множества  , если
, если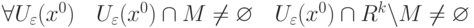 |
|
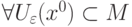 |
|
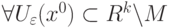 |
|
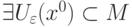 |
|
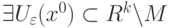 |
|
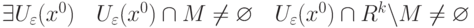 |
 - внутренняя точка множества
- внутренняя точка множества  . Тогда
. Тогда 
принадлежит множеству  |
|
граничная точка множества 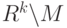 |
|
граничная точка множества  |
|
предельная точка множества  |
|
принадлежит множеству 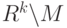 |
|
предельная точка множества 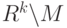 |
 является замкнутым, если
является замкнутым, если| любая его точка внутренняя | |
любая точка из его дополнения 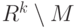 внутренняя внутренняя |
|
| некоторые его точки внутренние | |
некоторые точки из его дополнения 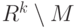 внутренние внутренние |
 называется предельной точкой множества
называется предельной точкой множества  , если
, если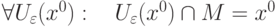 |
|
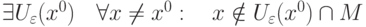 |
|
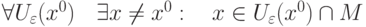 |
|
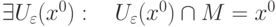 |
 называется открытым, если
называется открытым, если| некоторые его точки внутренние | |
любая точка из его дополнения 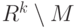 внутренняя внутренняя |
|
некоторые точки из его дополнения 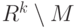 внутренние внутренние |
|
| любая его точка внутренняя |
последовательность вложенных замкнутых шаров в  имеет пустое пересечение имеет пустое пересечение |
|
| в каждый открытый шар можно вписать замкнутый параллелепипед | |
последовательность вложенных замкнутых шаров в  имеет непустое пересечение имеет непустое пересечение |
|
последовательность вложенных открытых шаров в  имеет пустое пересечение имеет пустое пересечение |
|
последовательность вложенных открытых шаров в  имеет непустое пересечение имеет непустое пересечение |
| пересечение любой совокупности замкнутых множеств | |
окрестность  |
|
пространство  |
|
| множество предельных точек множества | |
| объединение любой совокупности замкнутых множеств | |
| объединение конечного числа замкнутых множеств |
 не является точкой экстремума функции
не является точкой экстремума функции  при условии
при условии 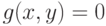 . Тогда линия уровня
. Тогда линия уровня 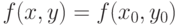 пересекает кривую
пересекает кривую  под углом
под углом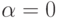 |
|
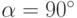 |
|
 |
 являются
являютсяконцентрические сферы с центром в точке 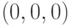 |
|
| концентрические сферы с центром в любой точке | |
концентрические сферы с центром в точке  |
|
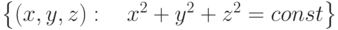 |
 определяет уравнение
определяет уравнение 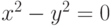 в окрестности точки
в окрестности точки  :
:| четыре | |
| одна | |
| две | |
| ни одной |
 , лежащая на кривой
, лежащая на кривой  , является точкой условного максимума, если существует окрестность
, является точкой условного максимума, если существует окрестность  :
: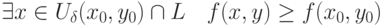 |
|
 |
|
 |
|
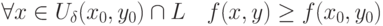 |
 . Какие утверждения верны:
. Какие утверждения верны: открытое множество открытое множество |
|
 счетное множество счетное множество |
|
 имеет только 1 предельную точку имеет только 1 предельную точку |
 - особая точка для дифференцируемой функции
- особая точка для дифференцируемой функции  . Какое условие является достаточным для того, чтобы
. Какое условие является достаточным для того, чтобы  была точкой локального минимума:
была точкой локального минимума: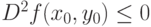 |
|
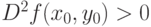 |
|
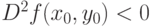 |
|
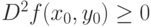 |
|
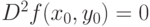 |
 . Какие утверждения верны:
. Какие утверждения верны:если 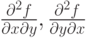 в точке в точке  , то , то 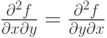 |
|
если 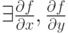 в точке в точке  , то , то 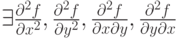 в точке в точке  |
|
если 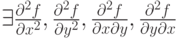 в точке в точке  , то , то 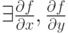 в точке в точке  |
|
если 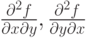 непрерывны в точке непрерывны в точке  , то , то 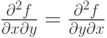 |
 не является точкой локального максимума для функции
не является точкой локального максимума для функции  , если для любой окрестности
, если для любой окрестности  :
: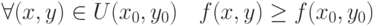 |
|
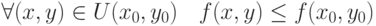 |
|
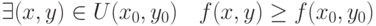 |
|
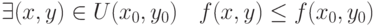 |
 - множество иррациональных чисел. Какие утверждения верны:
- множество иррациональных чисел. Какие утверждения верны: - замкнутое множество - замкнутое множество |
|
 не является открытым не является открытым |
|
| любая его точка является граничной | |
 содержит хотя бы одну изолированную точку содержит хотя бы одну изолированную точку |
 сходится,
сходится, 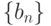 расходится. Тогда последовательность
расходится. Тогда последовательность 
| всегда сходится | |
| может сходится или расходится | |
| всегда расходится |
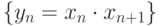 , если
, если  . Выберете правильные ответ:
. Выберете правильные ответ: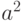 |
|
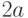 |
|
 |
|
 |
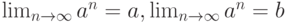 . Тогда
. Тогда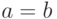 |
|
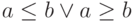 |
|
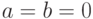 |
 и
и 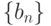 сходятся и
сходятся и  . Тогда последовательность
. Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен |
|
 |
|
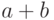 |
 сходящаяся и
сходящаяся и  . Тогда
. Тогда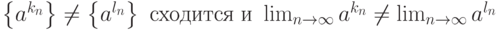 |
|
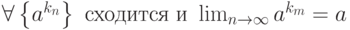 |
|
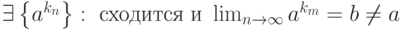 |
 - неограниченная последовательность в пространстве
- неограниченная последовательность в пространстве  . Какие утверждения верны:
. Какие утверждения верны: расходится расходится |
|
в некоторой окрестности лежит бесконечное число точек  |
|
из  можно выделить сходящуюся подпоследовательность можно выделить сходящуюся подпоследовательность |
 точек в
точек в  - это отображение
- это отображение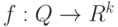 |
|
 |
|
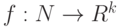 |
 называется пределом последовательности
называется пределом последовательности  ,если
,если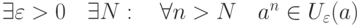 |
|
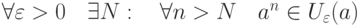 |
|
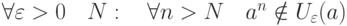 |
 состоит из одного элемента
состоит из одного элемента  . Тогда последовательность
. Тогда последовательность 
сходится и  |
|
сходится и 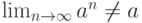 |
|
| расходится |
 ограничена.
ограничена.  - множество частичных пределов последовательности
- множество частичных пределов последовательности  . Какие утверждения верны:
. Какие утверждения верны: - замкнутое - замкнутое |
|
 - открытое - открытое |
|
 - ограничено - ограничено |
|
 - неограниченное - неограниченное |
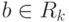 называется частичным пределом последовательности
называется частичным пределом последовательности  , если
, если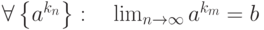 |
|
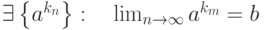 |
|
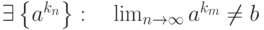 |
 . Тогда она
. Тогда она| немонотонная | |
| неубывающая | |
| невозрастающая | |
| ограниченная |
 сходится,
сходится, 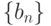 расходится. Тогда последовательность
расходится. Тогда последовательность 
| всегда сходится | |
| может сходится или расходится | |
| всегда расходится |
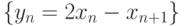 , если
, если  . Выберете правильные ответ:
. Выберете правильные ответ: |
|
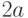 |
|
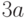 |
|
 |
 ограничена. Тогда
ограничена. Тогдалюбая подпоследовательность 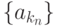 расходится расходится |
|
существует только одна сходящаяся подпоследовательность 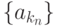 |
|
любая подпоследовательность 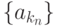 сходится сходится |
|
существует хотя бы одна сходящаяся подпоследовательность 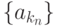 |
 сходящаяся. Какие утверждения верны:
сходящаяся. Какие утверждения верны:множество частичных пределов  бесконечно бесконечно |
|
множество частичных пределов  - пустое множество - пустое множество |
|
множество частичных пределов  состоит из состоит из  элементов элементов |
|
множество частичных пределов  состоит из одного элемента состоит из одного элемента |
 сходится и
сходится и  .
.  -множество частичных пределов
-множество частичных пределов  . Какие утверждения верны:
. Какие утверждения верны: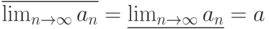 |
|
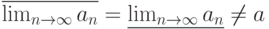 |
|
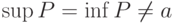 |
|
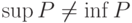 |
 , если
, если  . Выберете правильные ответ:
. Выберете правильные ответ: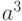 |
|
 |
|
 |
|
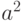 |
 ,
,  - множество частичных пределов
- множество частичных пределов  . Какие утверждения верны:
. Какие утверждения верны: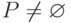 |
|
 неубывающая неубывающая |
|
 сходится сходится |
|
 ограничена сверху ограничена сверху |
|
 |
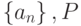 - множество частичных пределов
- множество частичных пределов  . Верхний предел числовой последовательности
. Верхний предел числовой последовательности  - это
- этоверхняя грань множества  , большая , большая 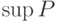 |
|
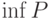 |
|
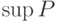 |
|
нижняя грань множества  , меньшая , меньшая 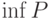 |
 . Какие утверждения верны:
. Какие утверждения верны: ограничена ограничена |
|
 неубывающая неубывающая |
|
 сходится сходится |
 . Пусть существует обратная к ней функция
. Пусть существует обратная к ней функция  . Какие утверждения справедливы:
. Какие утверждения справедливы: непрерывна в непрерывна в  или или 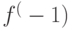 непрерывна в непрерывна в 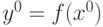 |
|
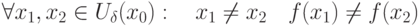 |
|
 непрерывна в непрерывна в  и и 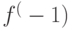 непрерывна в непрерывна в 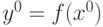 |
|
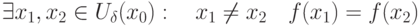 |
 является непрерывной:
является непрерывной: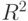 |
|
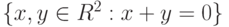 |
|
 |
|
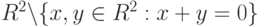 |
 называется пределом функции
называется пределом функции  при стремлениии
при стремлениии  , если
, если |
|
 |
|
 |
|
 |
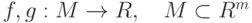 .
.  и
и  . Тогда функция
. Тогда функция  имеет предел и он равен
имеет предел и он равен |
|
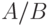 |
|
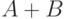 |
 называется непрерывной в точке
называется непрерывной в точке  , если
, если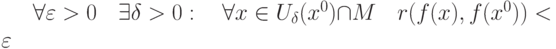 |
|
 |
|
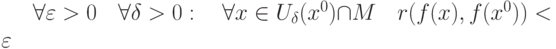 |
|
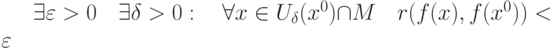 |
 . Пусть существует обратная к ней функция
. Пусть существует обратная к ней функция  . Какие утверждения справедливы:
. Какие утверждения справедливы: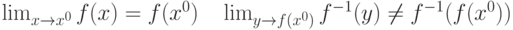 |
|
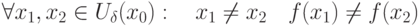 |
|
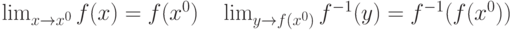 |
|
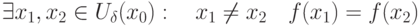 |
 . Какие утверждения справедливы:
. Какие утверждения справедливы: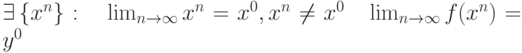 |
|
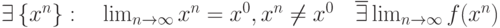 |
|
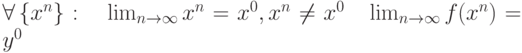 |
 называется непрерывной в точке
называется непрерывной в точке  , если
, если |
|
 |
|
 |
|
 |
 . Какие утверждения справедливы:
. Какие утверждения справедливы:если  непрерывная, то непрерывная, то  достигает своих верхней и нижней грани на достигает своих верхней и нижней грани на  , ,  - ограниченное множество - ограниченное множество |
|
если  непрерывная, то непрерывная, то  достигает своих верхней и нижней грани на достигает своих верхней и нижней грани на  , ,  - компакт - компакт |
|
если  непрерывная, то непрерывная, то  достигает своих верхней и нижней грани на достигает своих верхней и нижней грани на  , ,  - замкнутое множество - замкнутое множество |
 . Тогда
. Тогда 
ограничена в любой окрестности точки  |
|
| неограниченна | |
ограничена в некоторой окрестности точки  |
|
ограничена в открытом множестве, содержащем  |
 в пространстве
в пространстве  называется нефундаментальной, если
называется нефундаментальной, если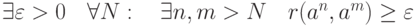 |
|
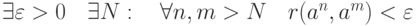 |
|
 |
|
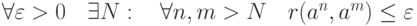 |
 является точкой локального минимума для функции
является точкой локального минимума для функции  при условиях
при условиях 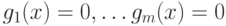 , если для
, если для  существует окрестность
существует окрестность  :
: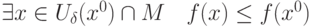 |
|
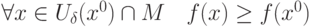 |
|
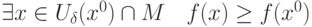 |
|
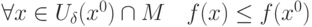 |
 в
в  и
и  .Тогда (по определению) это последовательность называется
.Тогда (по определению) это последовательность называется| ограниченной | |
| фундаментальной | |
| сходящейся |
 . Какие утверждения справедливы:
. Какие утверждения справедливы:если  непрерывная, то непрерывная, то  ограниченная на ограниченная на  , ,  - замкнутое множество - замкнутое множество |
|
если  ограниченная, то ограниченная, то  непрерывная непрерывная  , ,  - компактное множество - компактное множество |
|
если  непрерывная, то непрерывная, то  ограниченная на ограниченная на  , ,  - компактное множество - компактное множество |
|
если  ограниченная, то ограниченная, то  непрерывная непрерывная  , ,  - замкнутое множество - замкнутое множество |
 ,
,  - компактное множество. Какой может быть функция
- компактное множество. Какой может быть функция  на множестве
на множестве  :
:| разрывная и неограниченная | |
| непрерывная и неограниченная | |
| непрерывная и ограниченная |
 - компактное множество. Какой может быть функция
- компактное множество. Какой может быть функция  на множестве
на множестве  :
: непрерывная и непрерывная и  достигает своей верхней или нижней грани на достигает своей верхней или нижней грани на  |
|
 непрерывная и непрерывная и  не достигает своих верхней и нижней грани на не достигает своих верхней и нижней грани на  |
|
 разрывная и разрывная и  достигает своих верхней и нижней грани на достигает своих верхней и нижней грани на  |
|
 разрывная и разрывная и  не достигает своих верхней и нижней грани на не достигает своих верхней и нижней грани на  |
 . Для каких множеств
. Для каких множеств  справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность:
справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность: - ограниченное множество - ограниченное множество |
|
 - компактное множество - компактное множество |
|
 - замкнутое множество - замкнутое множество |
 - точка условного экстремума функции
- точка условного экстремума функции  и задана функция Лагранжа
и задана функция Лагранжа  . Тогда
. Тогда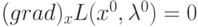 |
|
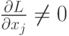 |
|
 |
 в точке
в точке 
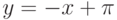 |
|
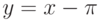 |
|
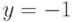 |
|
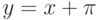 |
|
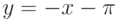 |
|
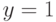 |
 - точка, в которой
- точка, в которой  или не существует. Какие утверждения верны:
или не существует. Какие утверждения верны: не является точкой экстремума не является точкой экстремума |
|
 - точка возможного экстремума - точка возможного экстремума |
|
 - точка локального экстремума - точка локального экстремума |
 и
и 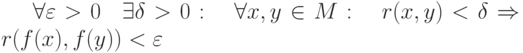 . Тогда функция
. Тогда функция  называется
называетсянепрерывной на множестве 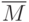 |
|
равномерно непрерывной на множестве 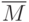 |
|
непрерывной на множестве  |
|
равномерно непрерывной на множестве  |
 непрерывная функция. Какие утверждения верны:
непрерывная функция. Какие утверждения верны:если  компактное множество, то и компактное множество, то и  компактное множество компактное множество |
|
если  замкнутое множество, то и замкнутое множество, то и  замкнутое множество замкнутое множество |
|
если  открытое множество, то и открытое множество, то и  открытое множество открытое множество |
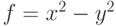 задана на множестве
задана на множестве  . Тогда
. Тогданаибольшее значение функции на множестве  достигается в точках достигается в точках 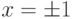 |
|
наибольшее значение функции на множестве  достигается более чем в одной точке достигается более чем в одной точке |
|
наибольшее значение функции на множестве  достигается только в одной точке достигается только в одной точке |
|
наибольшее значение функции на множестве  достигается в точке достигается в точке  |
 на множестве
на множестве  :
: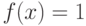 |
|
 |
|
 |
 сходился равномерно на множестве
сходился равномерно на множестве  :
: |
|
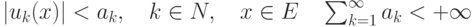 |
|
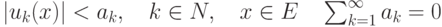 |
 сходится неравномерно на множестве
сходится неравномерно на множестве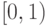 |
|
![(0,1]](http://www.intuit.ru/sites/default/files/tex_cache/668c7b55a37300c330dcd565d9e076da.png) |
|
![[0,1]](http://www.intuit.ru/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) |
 сходится к
сходится к  равномерно на множестве
равномерно на множестве  , если
, если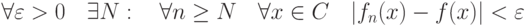 |
|
 |
|
 |
|
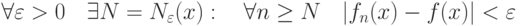 |
 называется точкой сходимости функциональной последовательности
называется точкой сходимости функциональной последовательности 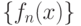 , если
, если |
|
числовая последовательность  сходится сходится |
|
числовая последовательность  расходится расходится |
|
 |
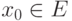 , если
, если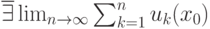 |
|
числовой ряд 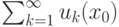 сходится сходится |
|
числовой ряд 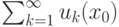 расходится расходится |
|
 |
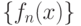 сходится к
сходится к  неравномерно на множестве
неравномерно на множестве  , если она
, если онасходится к  и и 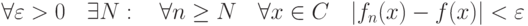 |
|
сходится к  и и  |
|
не сходится к  и и  |
|
не сходится к  и и 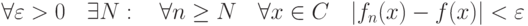 |
 сходится равномерно к функции
сходится равномерно к функции  на множестве
на множестве  тогда и только тогда, когда
тогда и только тогда, когда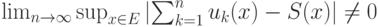 |
|
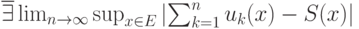 |
|
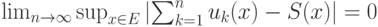 |
|
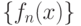 равномерно сходится к
равномерно сходится к  на множестве
на множестве  . Какие утверждения верны:
. Какие утверждения верны:если 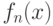 непрерывны на непрерывны на  , то , то  непрерывна на непрерывна на  |
|
если 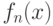 разрывны на разрывны на  , то , то  разрывна на разрывна на  |
|
последовательность разрывных на  функций функций 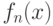 может сходиться к непрерывной может сходиться к непрерывной  |
|
последовательность ограниченных на  функций функций 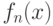 сходится к неограниченной сходится к неограниченной  |
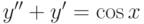 |
|
 |
|
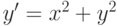 |
 непрерывна и удовлетворяет условию Липшица в некоторой окрестности
непрерывна и удовлетворяет условию Липшица в некоторой окрестности  и
и 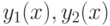 - решения задачи Коши
- решения задачи Коши  , то
, то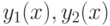 в некоторой окрестности в некоторой окрестности  |
|
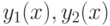 на всей области определения на всей области определения |

![[-1,1]](http://www.intuit.ru/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) |
|
| вся числовая прямая | |
 |
 :
: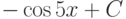 |
|
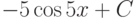 |
|
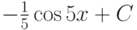 |
 решение
решение  является продолжением решения
является продолжением решения  . Тогда
. Тогда |
|
 |
|
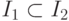 |
 . Тогда
. Тогдав любой окрестности  выполнено условие Липшица выполнено условие Липшица |
|
| решение задачи существует, но не единственно | |
| через начало координат проходит единственная интегральная кривая данного уравнения |
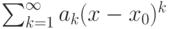 равен
равен![\underline{\lim_{n\rightarrow\infty}}\sqrt[n]{|a_n|}<+\infty](http://www.intuit.ru/sites/default/files/tex_cache/ce42920367588c02fa80e25b8a03d26a.png) |
|
![\overline{\lim_{n\rightarrow\infty}}\sqrt[n]{|a_n|}<+\infty](http://www.intuit.ru/sites/default/files/tex_cache/72d6b45bed895a814d00ba643b91444e.png) |
|
![\underline{\lim_{n\rightarrow\infty}}\frac{1}{\sqrt[n]{|a_n|}}<+\infty](http://www.intuit.ru/sites/default/files/tex_cache/34cf060ec2c37d97e82709321651d5b7.png) |
|
![\overline{\lim_{n\rightarrow\infty}}\frac{1}{\sqrt[n]{|a_n|}}<+\infty](http://www.intuit.ru/sites/default/files/tex_cache/3934a34cb0989bb18bfe8c0957634b80.png) |
 - интервал сходимости степенного ряда
- интервал сходимости степенного ряда  . Тогда
. Тогдаесли 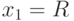 , то ряд сходится , то ряд сходится |
|
ряд сходится в точке  |
|
если 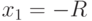 , то ряд расходится , то ряд расходится |
![\overline{\lim_{n\rightarrow\infty}}\frac{1}{\sqrt[n]{|a_n|}}=0](http://www.intuit.ru/sites/default/files/tex_cache/ddf35819a71b0020954b73df847aa2ca.png) , то интервал сходимости ряда
, то интервал сходимости ряда 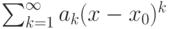
равен интервалу 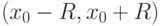 |
|
вырождается в одну точку  |
|
| равен числовой прямой |
 :
: |
|
 |
|
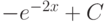 |
 :
: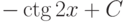 |
|
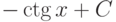 |
|
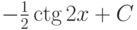 |
|
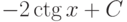 |
 - интервал сходимости степенного ряда
- интервал сходимости степенного ряда  . Тогда
. Тогдаряд расходится в точке  |
|
если 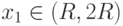 , то ряд сходится , то ряд сходится |
|
если 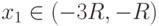 , то ряд расходится , то ряд расходится |
 является
является| линейным уравнением | |
| уравнением с разделяющимися переменными | |
| однородным уравнением |
 решение
решение  является продолжением решения
является продолжением решения  . Тогда
. Тогда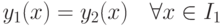 |
|
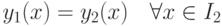 |
|
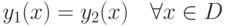 |
 может быть продолжено
может быть продолженона всю область определения  |
|
до границы замкнутого подмножества 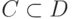 |
|
до границы компактного подмножества 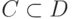 |
|
до границы ограниченного подмножества 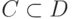 |
 - подмножество интервала сходимости. Тогда ряд сходится на множестве равномерно, если оно
- подмножество интервала сходимости. Тогда ряд сходится на множестве равномерно, если оно| компактное | |
| произвольное | |
| замкнутое | |
| ограниченное |
 . Какие утверждения верны:
. Какие утверждения верны:интервал сходимости ряда – множество  |
|
| на концах интервала сходимости ряд расходится | |
| сумма ряда неограниченна в окрестности 1 | |
| на концах интервала сходимости ряд сходится | |
ряд сходится равномерно на  |
 верны:
верны:если 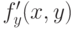 ограничена в окрестности ограничена в окрестности  , то решение задачи Коши существует и единственно , то решение задачи Коши существует и единственно |
|
если  непрерывна в окрестности непрерывна в окрестности  , то решение задачи Коши существует и единственно , то решение задачи Коши существует и единственно |
|
если  непрерывна и не удовлетворяет условию Липшица в окрестности непрерывна и не удовлетворяет условию Липшица в окрестности  , то решение задачи Коши существует, но он не единственно , то решение задачи Коши существует, но он не единственно |
| каждый степенной ряд имеет ненулевой интервал сходимости | |
| интервал сходимости степенного ряда может равняться одной точке | |
| каждый степенной ряд является функциональным | |
| интервал сходимости степенного ряда может равняться числовой прямой | |
| каждый функциональный ряд является степенным |