 содержащая множества
содержащая множества  и
и  . Укажите множества, принадлежащие
. Укажите множества, принадлежащие  .
.Ответы на курс: Введение в теорию вероятностей
 содержащая множества
содержащая множества  и
и  . Укажите множества, принадлежащие
. Укажите множества, принадлежащие  .
.
 |
|
 |
|
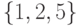 |
|
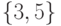 |
| 0,184 | |
| 0,271 | |
| 0,002 | |
| 0,368 |
| 0,271 | |
| 0,184 | |
| 0,002 | |
| 0,368 |
| 56/66 | |
| 1/65 | |
| 1/66 | |
| 6!/66 |
| 7 · 0,97 · 0,1 | |
| 8 · 0,97 · 0,1 | |
| 1 - 0,98 | |
| 0,97 · 0,1 |
| 0,243 | |
| 0,81 | |
| 0,1 | |
| 0,081 |
| (0, 1)13 | |
| 0, 1 | |
| 13 · (0, 1)13 | |
| (0, 1)12 |
| (5/6)6 | |
| 1 - (1/6)7 | |
| (5/6)5 | |
| 1 |
| 5/32 | |
| 1/32 | |
| 5/6 | |
| 1/16 |
| 1 | |
| 1/6 | |
| (5/6)29 · (1/6) | |
| 5 · (5/6)30 |
 |
|
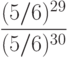 |
|
 |
|
 |
| 15/215 | |
| 15!/215 | |
| 1/2 | |
| 1/215 |
 принимает только значения
принимает только значения 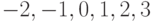 с одинаковой вероятностью
с одинаковой вероятностью  . Найдите
. Найдите 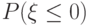 .
.| 0,5 | |
| 1 | |
| 1/6 | |
| 0 |
если  , то распределения случайных величин , то распределения случайных величин  и и 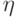 совпадают совпадают |
|
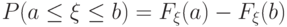 |
|
| сингулярное распределение может быть сосредоточено на множестве рациональных чисел | |
| плотность абсолютно непрерывного распределения в любой точке равна производной от функции распределения |
 задано функцией распределения:
задано функцией распределения: Выберите верные утверждения.
Выберите верные утверждения.
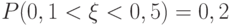 |
|
 |
|
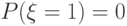 |
|
 |
|
 |
 задано плотностью распределения:
задано плотностью распределения: Выберите верные утверждения.
Выберите верные утверждения.
 |
|
 |
|
 |
|
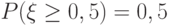 |
 задано функцией распределения:
задано функцией распределения: Выберите верные утверждения.
Выберите верные утверждения.
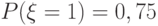 |
|
 |
|
 |
|
 |
|
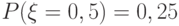 |
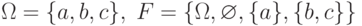 . Какие из следующих функций являются случайными величинами?
. Какие из следующих функций являются случайными величинами?
 |
|
 |
|
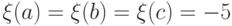 |
|
 |
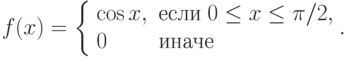 |
|
 |
|
 |
|
![f(x)=\left\{\begin{array}{ll}2, & \text{если}\;x\in[0;1],\\ -1, & \text{если}\;x\in(1;2],\\ 0, & \text{иначе} \end{array}\raght.](http://www.intuit.ru/sites/default/files/tex_cache/ae1c0d239f2145cf12045b851924c71b.png) |
 задано плотностью распределения:
задано плотностью распределения: Выберите верные утверждения.
Выберите верные утверждения.
 |
|
 |
|
 |
|
 |
 является наибольшей среди перечисленных.
является наибольшей среди перечисленных.
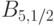 |
|
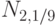 |
|
 |
|
 |
| биномиальное с параметрами 6 и 1/6 | |
| равномерное на отрезке от 0 до 6 | |
| распределение Пуассона с параметром 6 | |
| геометрическое с параметром 1/6 |
 |
|
 |
|
 |
|
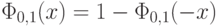 |
 имеет показательное распределение с параметром 2. Вычислите следующие вероятности и укажите верное неравенство.
имеет показательное распределение с параметром 2. Вычислите следующие вероятности и укажите верное неравенство.
 |
|
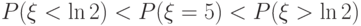 |
|
 |
|
 |
 является наибольшей среди перечисленных.
является наибольшей среди перечисленных.
 |
|
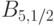 |
|
 |
|
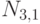 |
 имеет нормальное распределение с плотностью распределения
имеет нормальное распределение с плотностью распределения 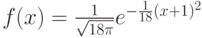 . Пусть
. Пусть  — функция распределения стандартного нормального распределения. Чему равно значение вероятности
— функция распределения стандартного нормального распределения. Чему равно значение вероятности  ?
?
 |
|
 |
|
 |
|
 |
 равна числу черных шаров среди выбранных. Вычислите следующие вероятности и укажите верное неравенство.
равна числу черных шаров среди выбранных. Вычислите следующие вероятности и укажите верное неравенство.
 |
|
 |
|
 |
|
 |
 равна сумме выпавших очков, случайная величина
равна сумме выпавших очков, случайная величина 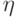 равна числу выпавших единиц. Укажите вероятность события
равна числу выпавших единиц. Укажите вероятность события  .
.| 5/36 | |
| 1/18 | |
| 1/36 | |
| 1/12 | |
| 125/1296 |
| зная частные распределения, можно найти функцию совместного распределения | |
| функция совместного распределения не убывает по каждой переменной | |
| зная функцию совместного распределения, можно найти частные функции распределения | |
| функция совместного распределения непрерывна по каждой переменной |
 и
и 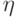 с дискретными распределениями.
с дискретными распределениями.
 |
|
 |
|
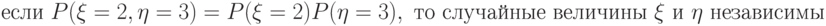 |
|
 |
 равна сумме выпавших очков, случайная величина
равна сумме выпавших очков, случайная величина 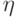 равна числу выпавших единиц. Укажите вероятность события
равна числу выпавших единиц. Укажите вероятность события 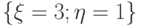 .
.| 1/12 | |
| 1/36 | |
| 1/18 | |
| 5/324 | |
| 5/36 |
 имеет абсолютно непрерывное распределение с постоянной плотностью во всех точках ромба
имеет абсолютно непрерывное распределение с постоянной плотностью во всех точках ромба  . Вне ромба плотность нулевая. Каково значение плотности внутри ромба?
. Вне ромба плотность нулевая. Каково значение плотности внутри ромба?| 1/? | |
| 1/2 | |
| 1 | |
| 1/2? |
 равна сумме выпавших очков, случайная величина
равна сумме выпавших очков, случайная величина 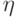 равна числу выпавших двоек. Укажите вероятность события
равна числу выпавших двоек. Укажите вероятность события  .
.| 5/162 | |
| 5/36 | |
| 1/12 | |
| 1/36 | |
| 1/18 |
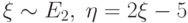 . Укажите значение плотности распределения случайной величины
. Укажите значение плотности распределения случайной величины 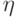 в точке
в точке 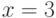 .
.
 |
|
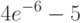 |
|
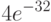 |
|
 |
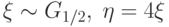 . Укажите значение вероятности
. Укажите значение вероятности 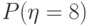 .
.| 1/4 | |
| 1/32 | |
| 1/6 | |
| 1/8 |
 имеет абсолютно непрерывное распределение с плотностью
имеет абсолютно непрерывное распределение с плотностью  . Пусть
. Пусть  . Какова плотность распределения случайной величины
. Какова плотность распределения случайной величины 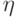 ?
?
 |
|
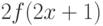 |
|
 |
|
 |
 . Укажите распределение случайной величины
. Укажите распределение случайной величины 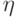 .
.
 |
|
 |
|
 |
|
 |
 с одним и тем же распределением Бернулли с параметром 1/2. Найдите
с одним и тем же распределением Бернулли с параметром 1/2. Найдите  .
.| 1/8 | |
| 5/16 | |
| 1/32 | |
| 0 |
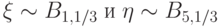 .
.
 |
|
 |
|
 |
|
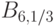 |
| тогда график ее плотности сдвинется вправо на 5 | |
| тогда график ее плотности сдвинется влево на 5 | |
| тогда график ее функции распределения сдвинется влево на 5 | |
| тогда график ее функции распределения сдвинется вправо на 5 |
 . Укажите значение плотности распределения случайной величины
. Укажите значение плотности распределения случайной величины 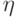 в точке
в точке 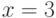 .
.| 1/3 | |
| 0 | |
| 1 | |
| 5 |
 .
.
 |
|
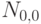 |
|
 |
|
 |
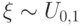 . Укажите, какая из следующих случайных величин имеет распределение
. Укажите, какая из следующих случайных величин имеет распределение  .
.
 |
|
 |
|
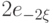 |
|
 |
 , если случайная величина
, если случайная величина  имеет распределение с плотностью
имеет распределение с плотностью
| e1/3 | |
| 1/3 | |
| 3/2 | |
| 1 |
 .
.| 1,2,4,3 | |
| 3,2,1,4 | |
| 3,1,4,2 | |
| 4,3,1,2 | |
| 2,3,1,4 |
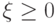 п. н. и указанные математические ожидания существуют, выберите верные неравенства.
п. н. и указанные математические ожидания существуют, выберите верные неравенства.
![\sqrt[5]{E\xi^5}\le\sqrt[4]{E\xi^4}](http://www.intuit.ru/sites/default/files/tex_cache/8226927850dffcbd579955142eba307c.png) |
|
 |
|
 |
|
 |
| распределение, плотность которого равна нулю вне некоторого отрезка [a, b] | |
распределение с функцией распределения  |
|
распределение с функцией распределения 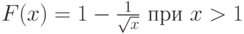 |
|
распределение 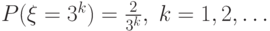 |
| математическое ожидание всегда неотрицательно | |
 существует тогда и только тогда, когда существует тогда и только тогда, когда  |
|
| если существует математическое ожидание случайной величины, то существует и дисперсия | |
| если случайная величина может принимать сколь угодно большие значения, то ее математическое ожидание не существует |
распределение  |
|
распределение с плотностью  |
|
распределение с плотностью  |
|
распределение с плотностью 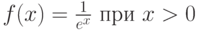 |
 , если случайная величина
, если случайная величина  имеет таблицу распределения
имеет таблицу распределения 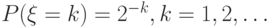
| 1/4 | |
| 4/3 | |
| 1/3 | |
| 1/2 |
| 2 | |
| 1,4 | |
| 1 | |
| 3 | |
| 0,09 |
 и
и 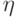 имеют конечные и ненулевые дисперсии и связаны равенством
имеют конечные и ненулевые дисперсии и связаны равенством  . Укажите значение их коэффициента корреляции.
. Укажите значение их коэффициента корреляции.| -1 | |
| 1 | |
| 2 | |
| 0 |
 и
и 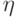 имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
имеют конечные и ненулевые дисперсии. Укажите верные утверждения.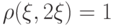 |
|
если  п. н., то п. н., то  |
|
если  , то случайные величины , то случайные величины  независимы независимы |
|
если  , то случайные величины , то случайные величины  и и 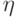 независимы независимы |
 и
и 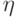 независимы и имеют одно и то же равномерное распределение на отрезке [0, 1]. Найдите коэффициент корреляции случайных величин
независимы и имеют одно и то же равномерное распределение на отрезке [0, 1]. Найдите коэффициент корреляции случайных величин  .
. |
|
 |
|
| 0 | |
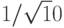 |
|
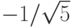 |
 и
и 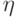 независимы и имеют стандартное нормальное распределение. Укажите значение их коэффициента корреляции.
независимы и имеют стандартное нормальное распределение. Укажите значение их коэффициента корреляции.| 1 | |
| 0 | |
| 2 | |
| -1 |
 |
|
 |
|
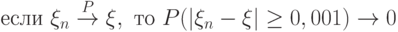 |
|
 |
 . Выберите достаточные условия для сходимости
. Выберите достаточные условия для сходимости  .
.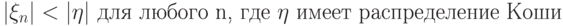 |
|
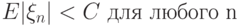 |
|
 |
|
 |
 имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром  . Вероятность
. Вероятность  можно оценить сверху по обобщенному неравенству Чебышева с помощью функции
можно оценить сверху по обобщенному неравенству Чебышева с помощью функции  . Укажите значение этой оценки.
. Укажите значение этой оценки.| 1/e2 | |
| 1/210 | |
| 1 | |
| e2/210 |
 . Укажите, каким числом оценивется по неравенству Чебышева вероятность
. Укажите, каким числом оценивется по неравенству Чебышева вероятность  .
.| 1/27 | |
| 1 | |
| 1/9 | |
| 1/3 |
 . Оценивается сверху вероятность
. Оценивается сверху вероятность  . Укажите значение оценки по обобщенному неравенству Чебышева с функцией
. Укажите значение оценки по обобщенному неравенству Чебышева с функцией  .
.| 0, 06 | |
| 1 | |
| 0, 05 | |
| 0, 1 |
 подбрасываний этих трех монет обозначим через
подбрасываний этих трех монет обозначим через  количество подбрасываний, при которых выпало не более одного герба. Укажите, чему равен предел при
количество подбрасываний, при которых выпало не более одного герба. Укажите, чему равен предел при  последовательности
последовательности  в смысле сходимости по вероятности.
в смысле сходимости по вероятности.| 0 | |
| предела не существует | |
| 1/2 | |
| 1/6 | |
| 1/4 |
 — последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами
— последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами 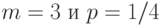 . Укажите, чему равен предел при
. Укажите, чему равен предел при  последовательности
последовательности в смысле сходимости почти наверное.
в смысле сходимости почти наверное.| 3/4 | |
| 0 | |
| 1/4 | |
| 9/16 | |
| 3/16 |
 имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром 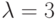 . Вероятность
. Вероятность  можно оценить сверху по обобщенному неравенству Чебышева с помощью функции
можно оценить сверху по обобщенному неравенству Чебышева с помощью функции  . Укажите значение этой оценки.
. Укажите значение этой оценки.| e6/310 | |
| 1/e3 | |
| e3/310 | |
| 1/310 |
 — последовательность независимых случайных величин с одним и тем же распределением Бернулли с параметром
— последовательность независимых случайных величин с одним и тем же распределением Бернулли с параметром  . Укажите, чему равен предел при
. Укажите, чему равен предел при  последовательности
последовательности в смысле сходимости по вероятности.
в смысле сходимости по вероятности.| 0 | |
| 1/4 | |
| 3/4 | |
| предела не существует или указанных условий недостаточно | |
| 1/2 |
 — последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами
— последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами 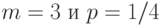 . Укажите, чему равен предел при
. Укажите, чему равен предел при  последовательности
последовательности в смысле сходимости по вероятности.
в смысле сходимости по вероятности.| 3/4 | |
| предела не существует или указанных условий недостаточно | |
| 0 | |
| 1/2 | |
| 1/4 |
 со следующими распределениями: для любого
со следующими распределениями: для любого 
 Найдите предел последовательности
Найдите предел последовательности  в смысле сходимости по вероятности.
в смысле сходимости по вероятности.| 0 | |
| 1 | |
 |
|
| 2 | |
| +? |
 . Оценивается сверху вероятность
. Оценивается сверху вероятность  . Укажите значение оценки по неравенству Маркова.
. Укажите значение оценки по неравенству Маркова.| 0, 1 | |
| 1 | |
| 0, 06 | |
| 0, 05 |
 . Выберите достаточные условия для сходимости
. Выберите достаточные условия для сходимости  .
. |
|
 |
|
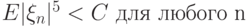 |
|
 |
 ,
,  - сумма первых
- сумма первых  случайных величин в этой последовательности. Последовательность
случайных величин в этой последовательности. Последовательность  слабо сходится к некоторому распределению. Найдите это распределение.
слабо сходится к некоторому распределению. Найдите это распределение.
 |
|
 |
|
 |
|
 |
|
 |
 со следующими распределениями:
со следующими распределениями:  . Если последовательность
. Если последовательность  слабо сходится к некоторому распределению, найдите это распределение.
слабо сходится к некоторому распределению, найдите это распределение.| последовательность не сходится по распределению | |
 |
|
 |
|
 |
 |
|
 |
|
 |
|
 |
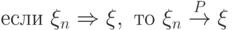 |
|
 |
|
 |
|
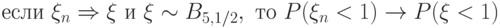 |
 со следующими распределениями:
со следующими распределениями:  . Если последовательность
. Если последовательность  слабо сходится к некоторому распределению, найдите это распределение.
слабо сходится к некоторому распределению, найдите это распределение.
 |
|
| последовательность не сходится по распределению | |
 |
|
 |
 |
|
 |
|
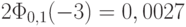 |
|
 |
|
 |
распределение с плотностью  при при  |
|
распределение с плотностью  при при  |
|
| равномерное распределение на отрезке [0, 1] |
 независимых в совокупности и одинаково распределјнных случайных величин с характеристической функцией
независимых в совокупности и одинаково распределјнных случайных величин с характеристической функцией  .
.
 |
|
 |
|
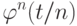 |
|
 |
 принимает значения ±1 с вероятностями по 1/2. Найдите характеристическую функцию
принимает значения ±1 с вероятностями по 1/2. Найдите характеристическую функцию  .
.
 |
|
 |
|
 |
|
 |
 .
.
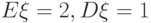 |
|
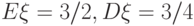 |
|
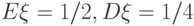 |
|
 |
|
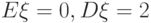 |
 .
.
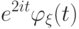 |
|
 |
|
 |
|
 |
 .
.
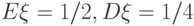 |
|
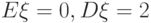 |
|
 |
|
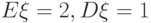 |
|
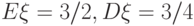 |
 и
и 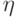 независимы. Чему равна характеристическая функция их суммы?
независимы. Чему равна характеристическая функция их суммы?| разности характеристических функций | |
| произведению характеристических функций | |
| сумме характеристических функций | |
| частному характеристических функций |
 .
.
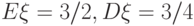 |
|
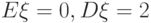 |
|
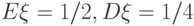 |
|
 |
|
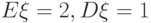 |
 .
.| 1 | |
 |
|
 |
|
| 0 |
 |
|
 |
|
 |
|
 |
|
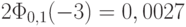 |
 |
|
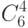 |
|
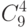 |
|
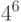 |
|
 |
| 12 | |
| 60 | |
| 3 | |
| 220 |
 |
|
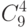 |
|
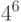 |
|
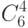 |
|
 |
| 120 | |
| 6 | |
| 20 | |
| 64 | |
| 8 |
| 3 | |
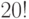 |
|
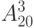 |
|
 |
|
 |
 — на первой монете выпал герб,
— на первой монете выпал герб,  — на второй монете выпал герб,
— на второй монете выпал герб,  — выпал хотя бы один герб. Выберите все верные высказывания.
— выпал хотя бы один герб. Выберите все верные высказывания.
 |
|
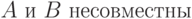 |
|
 |
|
 |
| невозможное событие совместно с самим собой | |
| пересечение любого числа попарно несовместных событий невозможно | |
| несовместные события противоположны | |
| противоположные события несовместны | |
| невозможное событие несовместно с любым другим |
| 7/8 | |
| 1/16 | |
| 1/2 | |
| 3/8 |
| 2/7 | |
| 1/7 | |
| 5/7 | |
| 4/5 |
| 1/36 | |
| 1/6 | |
| 1/4 | |
| 1/9 |
| 1/60 | |
| 1/40 | |
| 1/120 | |
| 1/20 |
| 0, 1 | |
| 0, 01 | |
| 0, 09 | |
| 0, 81 |
| 1/3 | |
| 4/7 | |
| 2/7 | |
| 1/7 |
| 1/7 | |
| 4/7 | |
| 2/7 | |
| 1/3 |
| 2/35 | |
| 1/18 | |
| 1/16 | |
| 1/4 |
 наудачу бросается на отрезок
наудачу бросается на отрезок ![[0, 1]](http://www.intuit.ru/sites/default/files/tex_cache/264884439b70ab09a86bc848421c6de6.png) . Выберите верные высказывания.
. Выберите верные высказывания.
 |
|
 |
|
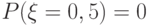 |
|
 |
| 6 | |
| 4 | |
| 5 | |
| 3 |
| 0,25 | |
| 0,2 | |
| 0,75 | |
| 0,5 |
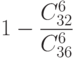 |
|
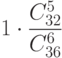 |
|
 |
|
 |
 |
|
 |
|
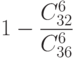 |
|
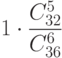 |
 и
и  — произвольные события, причем
— произвольные события, причем  влечет
влечет  . Выберите верное высказывание:
. Выберите верное высказывание:
 |
|
 |
|
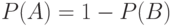 |
|
 |
 обозначает меру Лебега борелевского множества
обозначает меру Лебега борелевского множества  . Укажите значение
. Укажите значение 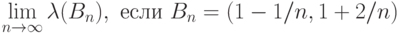 .
.| 0 | |
| 2 | |
| 1 | |
| 3 |
| 0,45 | |
| 0,7 | |
| 0,12 | |
| 0,5 |
 и
и  , для которых
, для которых  .
.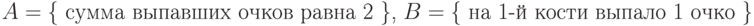 |
|
 |
|
 |
|
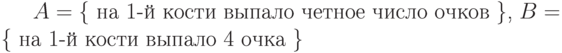 |
 и
и  .
.
 |
|
 |
|
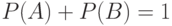 |
 . Какие из следующих множеств образуют алгебры подмножеств
. Какие из следующих множеств образуют алгебры подмножеств  ?
?| множество натуральных чисел | |
множество всех одноточечных подмножеств множества  |
|
множество всех подмножеств множества  |
|
множество всех интервалов  |
 — произвольное непустое множество. Укажите верные высказывания.
— произвольное непустое множество. Укажите верные высказывания.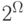 является алгеброй является алгеброй |
|
существуют алгебры, не являющиеся  -алгебрами -алгебрами |
|
существуют  - алгебры, не являющиеся алгебрами - алгебры, не являющиеся алгебрами |
|
 -алгебра всегда содержит бесконечное число множеств -алгебра всегда содержит бесконечное число множеств |
 такие, что
такие, что  ,
,  ,
,  . Укажите значение
. Укажите значение  .
.| 3/2 | |
| 3/4 | |
| 1 | |
| 7/8 |
 для произвольных событий
для произвольных событий  и
и  ?
?
 |
|
 |
|
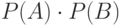 |
|
 |
 такие, что
такие, что 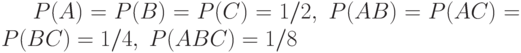 . Укажите значение
. Укажите значение  .
.| 3/2 | |
| 3/4 | |
| 1 | |
| 7/8 |
 содержащая множества
содержащая множества  и
и  . Укажите множества, принадлежащие
. Укажите множества, принадлежащие  .
.
 |
|
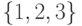 |
|
 |
|
 |
 . Выберите функции, которые являются вероятностными мерами.
. Выберите функции, которые являются вероятностными мерами.
 |
|
 |
|
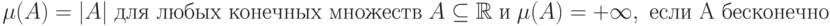 |
|
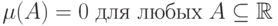 |
| 1/3 | |
| 1/4 | |
| 2/3 | |
| 1/2 |
| события A и B несовместны | |
| P(A ? B) = 1 | |
| P(A ? B) = 0 | |
| P(A|B) = 0, 5 |
| несовместные события независимы | |
| невозможное событие независимо с любым другим | |
| несовместные события зависимы | |
| несовместные события не пересекаются |
| 1/3 | |
| 1 | |
| 1/2 | |
| 1/6 |
| 0, 25 | |
| 0, 35 | |
| 0, 5 | |
| 0, 6 |
| 1/10 | |
| 2/3 | |
| 3/5 | |
| 3/16 |
| 1, 4 | |
| 0, 5 | |
| 0, 3 | |
| 0, 7 |