Ответы на курс: Введение в математический анализ
![\lim\limits_{n \to \infty} {\frac {\sqrt[3]{n^2 - 1}} {\sqrt[3]{n + 1} - \sqrt[3]{n}}}](http://www.intuit.ru/sites/default/files/tex_cache/fe94e876223ddbf7221862f418c108e3.png) равен
равен
Вычислить предел данной последовательности: ![\lim\limits_{n \to \infty} {[\frac {1} {3n} cos \frac {2} {n^2} - \frac {2n} {2-n}]}](http://www.intuit.ru/sites/default/files/tex_cache/b9273d961683dfcbc17b377191a4fed9.png)
Если  и
и  , то
, то
Функция  называется бесконечно малой функцией при
называется бесконечно малой функцией при  , стремящемся к
, стремящемся к  , если
, если 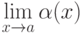 равен
равен
Если функция  непрерывна в точке
непрерывна в точке  и
и 
Как представить функцию  в виде композиции непрерывных функций
в виде композиции непрерывных функций  и
и 
Если функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то она на нём
, то она на нём
Если функция  непрерывна в точке
непрерывна в точке  , то односторонние пределы в этой точке
, то односторонние пределы в этой точке
Точка 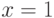 для функции
для функции  является точкой разрыва
является точкой разрыва
Пусть  . Сколько корней имеет данный многочлен:
. Сколько корней имеет данный многочлен:
Точка 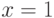 для функции
для функции  является точкой разрыва
является точкой разрыва
Если функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b], f(a) = A, f(b) = B](http://www.intuit.ru/sites/default/files/tex_cache/530663b6c2ab1bd03cb2a940588e60b8.png) то
то
Функция  непрерывна в точке
непрерывна в точке  , если односторонние пределы в этой точке
, если односторонние пределы в этой точке
Точка  называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если в этой точке
, если в этой точке 
Пусть 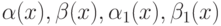 — бесконечно малые при
— бесконечно малые при  функции, причём
функции, причём  и
и 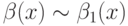 . Если
. Если  , то
, то
Что является асимптотической формулой для  при
при 
Пусть  . Тогда
. Тогда
Чему эквивалентна функция  при
при 
Чему эквивалентна функция  при
при 
Для какого множества из непрерывности функции на нём следует её равномерная непрерывность:
Пусть  б.м.ф. при
б.м.ф. при 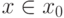 и
и  . Тогда
. Тогда
Б.м.ф.  при
при  имеет порядок малости
имеет порядок малости  , если
, если
Пусть 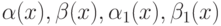 — бесконечно малые при
— бесконечно малые при  функции, причём
функции, причём  и
и 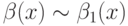 . Если
. Если 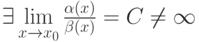 , то
, то
По определению (Коши), , если
, если 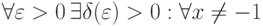
Функция  при
при  , если
, если
 при
при  является бесконечно большой, причем
является бесконечно большой, причем 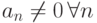 . Тогда
. Тогда  равен
равен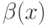 при
при 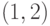 :
: . Тогда
. Тогда при
при 
