Ответы на курс: Математический анализ
Ответы на курс: Математический анализ
 и
и  , если
, если 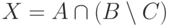 ,
, 
 называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве  , если
, если в точке с абсциссой
в точке с абсциссой  , равен
, равен является точкой разрыва
является точкой разрыва не является точкой локального минимума функции
не является точкой локального минимума функции  , если
, если является точкой локального максимума функции
является точкой локального максимума функции  , если
, если называется левым пределом
называется левым пределом 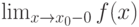 числовой функции
числовой функции  , если
, если является точкой локального минимума функции
является точкой локального минимума функции  , если
, если для функции
для функции  является точкой разрыва
является точкой разрыва существует и равен
существует и равен называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если в точке
, если в точке 
 в данной точке
в данной точке  называется
называется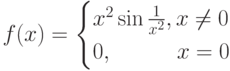 . Сколько точек пересечения касательной к графику функции в точке
. Сколько точек пересечения касательной к графику функции в точке  и графика функции в произвольной окрестности точки
и графика функции в произвольной окрестности точки 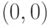 :
: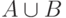 ,
,  если
если 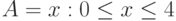 ,
, 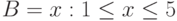 , если
, если в в виде
в в виде  , если
, если  и
и  — натуральные числа, не имеющие общих делителей.
— натуральные числа, не имеющие общих делителей. , то
, то элементов
элементов в в виде
в в виде  , если
, если  и
и  — натуральные числа, не имеющие общих делителей.
— натуральные числа, не имеющие общих делителей. — точка локального экстремума дифференцируемой функции
— точка локального экстремума дифференцируемой функции  . Тогда
. Тогда не является равномерно непрерывной на множестве
не является равномерно непрерывной на множестве  , если
, если является пределом
является пределом  числовой функции
числовой функции  . Какие утверждения верны:
. Какие утверждения верны: существует и равен
существует и равен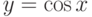 в точке
в точке 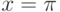
 — точка локального экстремума функции
— точка локального экстремума функции  . Тогда производная
. Тогда производная — непрерывна в точке
— непрерывна в точке  . Тогда
. Тогда![f(x)=x-[x],\quad 0\leq x\leq 1](http://www.intuit.ru/sites/default/files/tex_cache/3d73868a6fa1fc5f680c1edf55a2cdc7.png) , где
, где ![[x]](http://www.intuit.ru/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) — означает целую часть от числа:
— означает целую часть от числа: функции
функции  :
: называется дифференцируемой в точке
называется дифференцируемой в точке  , если
, если
 , в которой касательная
, в которой касательная непрерывна на
непрерывна на ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) и дифференцируема на
и дифференцируема на  . Какое утверждение верно:
. Какое утверждение верно: непрерывна на
непрерывна на  , дифференцируема на
, дифференцируема на  и
и  . Какие утверждения верны:
. Какие утверждения верны: функции
функции  , сама функция и остаточный член
, сама функция и остаточный член  :
: . Какие утверждения верны:
. Какие утверждения верны: :
: называется невозрастающей на
называется невозрастающей на 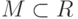 , если
, если 
 называется выпуклым, если
называется выпуклым, если функции
функции  :
: называется неубывающей на множестве
называется неубывающей на множестве 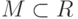 , если
, если 
![f(x)=\sqrt{x},\quad x\in[0,1]](http://www.intuit.ru/sites/default/files/tex_cache/82f277ce21f3a96d6c632a0f959b9c41.png) . Тогда
. Тогда для
для  раз дифференцируемой в окрестности точки
раз дифференцируемой в окрестности точки  функции
функции 
 непрерывна на
непрерывна на ![[a,b]](http://www.intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) и дифференцируема на
и дифференцируема на  . Какое утверждение верно:
. Какое утверждение верно: в точке
в точке  :
: называется выпуклой на множестве
называется выпуклой на множестве  (выпуклое), если
(выпуклое), если называется возрастающей на
называется возрастающей на 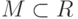 , если
, если 
![f(x,y)=\sqrt[3]{xy})](http://www.intuit.ru/sites/default/files/tex_cache/125cd39a13dce6a856a78e2f6d67fee1.png) . Какие утверждения верны:
. Какие утверждения верны: . Какие утверждения верны:
. Какие утверждения верны: .Какие утверждения верны:
.Какие утверждения верны: . На каких множествах существует неявная функция
. На каких множествах существует неявная функция 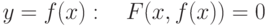 :
: . Уравнение касательной в точке
. Уравнение касательной в точке 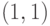 :
: . Тогда
. Тогда  равен
равен при условии
при условии 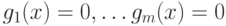 . Пусть задана функция Лагранжа
. Пусть задана функция Лагранжа  . Тогда особая точка
. Тогда особая точка  будет точкой условного локального минимума, если для любого допустимого сдвига
будет точкой условного локального минимума, если для любого допустимого сдвига в точке
в точке  и найти его модуль (длину):
и найти его модуль (длину): . Тогда частные производные 2 порядка равны:
. Тогда частные производные 2 порядка равны: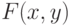 непрерывна в окрестности точки
непрерывна в окрестности точки  и
и  непрерывные в окрестности
непрерывные в окрестности  . Какие условия достаточны для существования единственной неявной функции
. Какие условия достаточны для существования единственной неявной функции  :
: является точкой локального минимума для функции
является точкой локального минимума для функции  , если существует окрестность
, если существует окрестность  :
: точка экстремума функции
точка экстремума функции  при условии
при условии 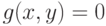 . Тогда линия уровня
. Тогда линия уровня 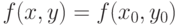 пересекает кривую
пересекает кривую  под углом
под углом равна:
равна: является точкой локального максимума для функции
является точкой локального максимума для функции  , если существует окрестность
, если существует окрестность  :
: , то
, то
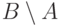 , если
, если 
 состоит из трех элементов, а множество
состоит из трех элементов, а множество  — из двух элементов. Сколько существует отображений
— из двух элементов. Сколько существует отображений  в
в  ?
? и
и  , если
, если 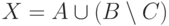 ,
, 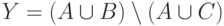

![M = [a,b]](http://www.intuit.ru/sites/default/files/tex_cache/ddbb2a46ecbb84583c79a3d672aefcc2.png) , то
, то в виде
в виде  , если
, если  и
и  — натуральные числа, не имеющие общих делителей.
— натуральные числа, не имеющие общих делителей.
 , удовлетворяющих неравенству
, удовлетворяющих неравенству 


 и
и  , если
, если 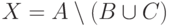 ,
, 
 называется изолированной точкой множества
называется изолированной точкой множества  , если
, если открытого шара
открытого шара  является множество
является множество называется ограниченным, если оно
называется ограниченным, если оно в
в 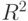 вычисляется по формуле
вычисляется по формуле — изолированная точка множества
— изолированная точка множества  . Какие утверждения верны:
. Какие утверждения верны:![G=(1,2)\cup\{3\}\cup(4,5]](http://www.intuit.ru/sites/default/files/tex_cache/28fd252433ae7c4b811044d1d69ce531.png) . Какое множество является множеством изолированных точек
. Какое множество является множеством изолированных точек  :
: в
в  вычисляется по формуле
вычисляется по формуле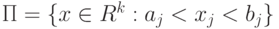 называется
называется называется компактным, если оно
называется компактным, если оно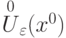 всех внутренних точек открытого шара
всех внутренних точек открытого шара![G=(1,2)\cup\{3\}\cup(4,5]](http://www.intuit.ru/sites/default/files/tex_cache/28fd252433ae7c4b811044d1d69ce531.png) . Какое множество является множеством граничных точек
. Какое множество является множеством граничных точек  :
: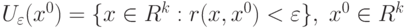 называется
называется![G=(1,2)\cup\{3\}\cup(4,5]](http://www.intuit.ru/sites/default/files/tex_cache/28fd252433ae7c4b811044d1d69ce531.png) . Какое множество является множеством предельных точек
. Какое множество является множеством предельных точек  :
: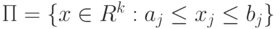 называется
называется точки
точки  называется
называется точки
точки  называется
называется открытого шара
открытого шара  является множество
является множество — множество рациональных чисел. Какие утверждения верны:
— множество рациональных чисел. Какие утверждения верны: в
в  вычисляется по формуле
вычисляется по формуле называется граничной точкой множества
называется граничной точкой множества  , если
, если — внутренняя точка множества
— внутренняя точка множества  . Тогда
. Тогда 
 является замкнутым, если
является замкнутым, если замкнуто. Какие утверждения верны:
замкнуто. Какие утверждения верны: называется внутренней точкой множества
называется внутренней точкой множества  , если
, если называется внешней точкой множества
называется внешней точкой множества  , если
, если называется предельной точкой множества
называется предельной точкой множества  , если
, если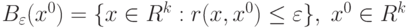 называется
называется называется открытым, если
называется открытым, если — множество натуральных чисел. Какие утверждения верны:
— множество натуральных чисел. Какие утверждения верны: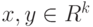 вычисляется по формуле
вычисляется по формуле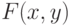 непрерывна в окрестности точки
непрерывна в окрестности точки  и
и 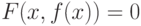 . Пусть существует единственная неявная функция
. Пусть существует единственная неявная функция  . Тогда
. Тогда не является точкой экстремума функции
не является точкой экстремума функции  при условии
при условии 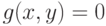 . Тогда линия уровня
. Тогда линия уровня 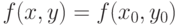 пересекает кривую
пересекает кривую  под углом
под углом являются
являются определяет уравнение
определяет уравнение 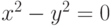 в окрестности точки
в окрестности точки  :
: , лежащая на кривой
, лежащая на кривой  , является точкой условного максимума, если существует окрестность
, является точкой условного максимума, если существует окрестность  :
: . Какие утверждения верны:
. Какие утверждения верны: — особая точка для дифференцируемой функции
— особая точка для дифференцируемой функции  . Какое условие является достаточным для того, чтобы
. Какое условие является достаточным для того, чтобы  была точкой локального минимума:
была точкой локального минимума: . Какие утверждения верны:
. Какие утверждения верны: . Тогда частные производные 2 порядка равны:
. Тогда частные производные 2 порядка равны: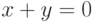 не определяет неявной функции в достаточно малой окрестности точки
не определяет неявной функции в достаточно малой окрестности точки 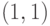 . Какое условие не выполнено:
. Какое условие не выполнено: не является точкой локального максимума для функции
не является точкой локального максимума для функции  , если для любой окрестности
, если для любой окрестности  :
: при условии
при условии 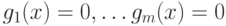 . Пусть задана функция Лагранжа
. Пусть задана функция Лагранжа  . Тогда особая точка
. Тогда особая точка  будет точкой условного локального максимума, если для любого допустимого сдвига
будет точкой условного локального максимума, если для любого допустимого сдвига — множество иррациональных чисел. Какие утверждения верны:
— множество иррациональных чисел. Какие утверждения верны: сходится,
сходится, 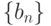 расходится. Тогда последовательность
расходится. Тогда последовательность 
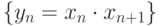 , если
, если  . Выберете правильные ответ:
. Выберете правильные ответ: . Какая последовательность натуральных чисел задает подпоследовательность
. Какая последовательность натуральных чисел задает подпоследовательность  :
: . Тогда вне каждой окрестности
. Тогда вне каждой окрестности 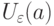 —
—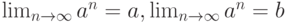 . Тогда
. Тогда и
и 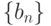 сходятся и
сходятся и  . Тогда последовательность
. Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен называется пределом числовой последовательности
называется пределом числовой последовательности  , если
, если сходящаяся и
сходящаяся и  . Тогда
. Тогда содержится конечное число элементов последовательности
содержится конечное число элементов последовательности  . Какие утверждения верны:
. Какие утверждения верны: — неограниченная последовательность в пространстве
— неограниченная последовательность в пространстве  . Какие утверждения верны:
. Какие утверждения верны: точек в
точек в  — это отображение
— это отображение . Тогда она
. Тогда она называется пределом последовательности
называется пределом последовательности  ,если
,если . Тогда последовательность
. Тогда последовательность 
 состоит из одного элемента
состоит из одного элемента  . Тогда последовательность
. Тогда последовательность 
 ограничена.
ограничена.  — множество частичных пределов последовательности
— множество частичных пределов последовательности  . Какие утверждения верны:
. Какие утверждения верны: ограничена.
ограничена.  — множество частичных пределов последовательности
— множество частичных пределов последовательности  . Какие утверждения верны:
. Какие утверждения верны: — сходящаяся к точке
— сходящаяся к точке  последовательность элементов замкнутого множества
последовательность элементов замкнутого множества  . Тогда
. Тогда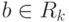 называется частичным пределом последовательности
называется частичным пределом последовательности  , если
, если . Тогда она
. Тогда она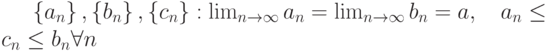 . Тогда
. Тогда 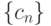
 и
и 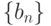 сходятся и
сходятся и  . Тогда последовательность
. Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен сходится,
сходится, 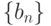 расходится. Тогда последовательность
расходится. Тогда последовательность 
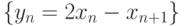 , если
, если  . Выберете правильные ответ:
. Выберете правильные ответ: — предельная точка множества
— предельная точка множества  , то
, то ограничена. Тогда
ограничена. Тогда сходящаяся. Какие утверждения верны:
сходящаяся. Какие утверждения верны: сходится и
сходится и  .
.  -множество частичных пределов
-множество частичных пределов  . Какие утверждения верны:
. Какие утверждения верны: , если
, если  . Выберете правильные ответ:
. Выберете правильные ответ: и
и 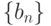 сходятся и
сходятся и  .Тогда последовательность
.Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен сходится и
сходится и  . Тогда
. Тогда . Тогда внутри каждой окрестности
. Тогда внутри каждой окрестности 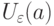 —
— ,
,  — множество частичных пределов
— множество частичных пределов  . Какие утверждения верны:
. Какие утверждения верны: — последовательность элементов компактного множества
— последовательность элементов компактного множества  . Какие утверждения верны:
. Какие утверждения верны: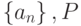 — множество частичных пределов
— множество частичных пределов  . Верхний предел числовой последовательности
. Верхний предел числовой последовательности  — это
— это . Какие утверждения верны:
. Какие утверждения верны: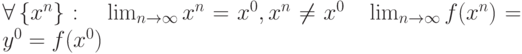 . Тогда
. Тогда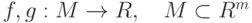 .
.  и
и  . Тогда функция
. Тогда функция  имеет предел и он равен
имеет предел и он равен . Пусть существует обратная к ней функция
. Пусть существует обратная к ней функция  . Какие утверждения справедливы:
. Какие утверждения справедливы: в пространстве
в пространстве  называется фундаментальной, если
называется фундаментальной, если является непрерывной:
является непрерывной: в пространстве
в пространстве  нефундаментальная. Какие утверждения верны:
нефундаментальная. Какие утверждения верны: называется пределом функции
называется пределом функции  при стремлениии
при стремлениии  , если
, если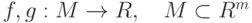 .
.  и
и  . Тогда функция
. Тогда функция  имеет предел и он равен
имеет предел и он равен![f(x):[a,b]\rightarrow R](http://www.intuit.ru/sites/default/files/tex_cache/3b22ca1a5b048519521640635627f2cb.png) . Пусть
. Пусть ![x_1,x_2\in[a,b]\quad f(x_1)=a_1,f(x_2)=a_2](http://www.intuit.ru/sites/default/files/tex_cache/d59668ed0657c8296a72b6063a2f827d.png) и
и 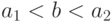 . Тогда
. Тогда . Тогда она
. Тогда она называется непрерывной в точке
называется непрерывной в точке  , если
, если . Пусть существует обратная к ней функция
. Пусть существует обратная к ней функция  . Какие утверждения справедливы:
. Какие утверждения справедливы: . Какие утверждения справедливы:
. Какие утверждения справедливы: называется непрерывной в точке
называется непрерывной в точке  , если
, если . Какие утверждения справедливы:
. Какие утверждения справедливы:![f(x):[a,b]\rightarrow R](http://www.intuit.ru/sites/default/files/tex_cache/3b22ca1a5b048519521640635627f2cb.png) . Пусть
. Пусть  . Тогда
. Тогда . Тогда
. Тогда 
 в пространстве
в пространстве  называется нефундаментальной, если
называется нефундаментальной, если в пространстве
в пространстве  сходится и
сходится и  . Какие утверждения верны:
. Какие утверждения верны: называется пределом функции
называется пределом функции  при стремлениии
при стремлениии  , если
, если является точкой локального минимума для функции
является точкой локального минимума для функции  при условиях
при условиях 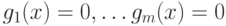 , если для
, если для  существует окрестность
существует окрестность  :
: в
в  и
и  .Тогда (по определению) это последовательность называется
.Тогда (по определению) это последовательность называется называется пределом функции
называется пределом функции  при стремлениии
при стремлениии  , если
, если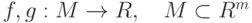 .
.  и
и  . Тогда функция
. Тогда функция  имеет предел и он равен
имеет предел и он равен . Какие утверждения справедливы:
. Какие утверждения справедливы: является непрерывной:
является непрерывной: ,
,  — компактное множество. Какой может быть функция
— компактное множество. Какой может быть функция  на множестве
на множестве  :
: — компактное множество. Какой может быть функция
— компактное множество. Какой может быть функция  на множестве
на множестве  :
:![f(x):[a,b]\rightarrow R](http://www.intuit.ru/sites/default/files/tex_cache/3b22ca1a5b048519521640635627f2cb.png)
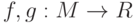 . Какие условия достаточны для того, чтобы функция
. Какие условия достаточны для того, чтобы функция  была непрерывной в точке
была непрерывной в точке  :
: дифференцируема в точке
дифференцируема в точке  и обратима в
и обратима в  и
и 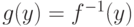 — обратная функция. Какие утверждения справедливы:
— обратная функция. Какие утверждения справедливы: . Для каких множеств
. Для каких множеств  справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность:
справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность: — особая точка для дифференцируемой функции
— особая точка для дифференцируемой функции  . Какое условие является достаточным для того, чтобы
. Какое условие является достаточным для того, чтобы  была точкой локального максимума:
была точкой локального максимума: является точкой локального максимума для функции
является точкой локального максимума для функции  при условиях
при условиях 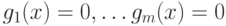 , если для
, если для  существует окрестность
существует окрестность  :
: — точка условного экстремума функции
— точка условного экстремума функции  и задана функция Лагранжа
и задана функция Лагранжа  . Тогда
. Тогда в точке с абсциссой
в точке с абсциссой  , равен
, равен в точке
в точке 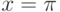
 обратима в окрестности точки
обратима в окрестности точки  и
и 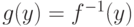 — обратная функция. Тогда производная
— обратная функция. Тогда производная  в точке
в точке  равна
равна — точка, в которой
— точка, в которой  или не существует. Какие утверждения верны:
или не существует. Какие утверждения верны: и
и 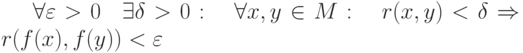 . Тогда функция
. Тогда функция  называется
называется для функции
для функции  является точкой разрыва
является точкой разрыва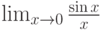 существует и равен
существует и равен непрерывная функция. Какие утверждения верны:
непрерывная функция. Какие утверждения верны: называется правым пределом
называется правым пределом  числовой функции
числовой функции  , если
, если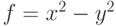 задана на множестве
задана на множестве  . Тогда
. Тогда на множестве
на множестве  :
: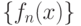 сходится к
сходится к  на множестве
на множестве  . Тогда
. Тогда :
: сходился равномерно на множестве
сходился равномерно на множестве  :
: сходится равномерно на множестве
сходится равномерно на множестве сходится неравномерно на множестве
сходится неравномерно на множестве по признаку Вейерштрасса:
по признаку Вейерштрасса: :
: на множестве
на множестве  :
: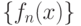 сходится к
сходится к  равномерно на множестве
равномерно на множестве  , если
, если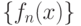 называется функциональной, если
называется функциональной, если называется выражение
называется выражение называется точкой сходимости функциональной последовательности
называется точкой сходимости функциональной последовательности 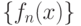 , если
, если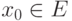 , если
, если по признаку Вейерштрасса:
по признаку Вейерштрасса: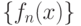 сходится к
сходится к  неравномерно на множестве
неравномерно на множестве  , если она
, если она :
:
 сходится равномерно к функции
сходится равномерно к функции  на множестве
на множестве  тогда и только тогда, когда
тогда и только тогда, когда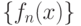 не сходится к
не сходится к  равномерно на множестве
равномерно на множестве  , если
, если
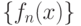 равномерно сходится к
равномерно сходится к  на множестве
на множестве  . Какие утверждения верны:
. Какие утверждения верны:
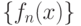 сходится равномерно к
сходится равномерно к  тогда и только тогда, когда
тогда и только тогда, когда сходится равномерно к функции
сходится равномерно к функции  на множестве
на множестве  . Тогда
. Тогда непрерывна и удовлетворяет условию Липшица в некоторой окрестности
непрерывна и удовлетворяет условию Липшица в некоторой окрестности  и
и 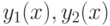 — решения задачи Коши
— решения задачи Коши  , то
, то — интервал сходимости степенного ряда
— интервал сходимости степенного ряда  . Тогда
. Тогда
 :
: :
: решение
решение  является продолжением решения
является продолжением решения  . Тогда
. Тогда является
является . Тогда
. Тогда![\overline{\lim_{n\rightarrow\infty}}\frac{1}{\sqrt[n]{|a_n|}}=+\infty](http://www.intuit.ru/sites/default/files/tex_cache/e792e0d067a9f672402e867f587bbf71.png) , то интервал сходимости ряда
, то интервал сходимости ряда 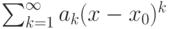
 интервал сходимости степенного ряда
интервал сходимости степенного ряда  . Тогда множеством непрерывности суммы ряда является множество
. Тогда множеством непрерывности суммы ряда является множество имеет решение
имеет решение  , то
, то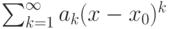 равен
равен — интервал сходимости степенного ряда
— интервал сходимости степенного ряда  . Тогда
. Тогда![\overline{\lim_{n\rightarrow\infty}}\frac{1}{\sqrt[n]{|a_n|}}=0](http://www.intuit.ru/sites/default/files/tex_cache/ddf35819a71b0020954b73df847aa2ca.png) , то интервал сходимости ряда
, то интервал сходимости ряда 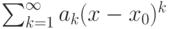
 :
: :
: — интервал сходимости степенного ряда
— интервал сходимости степенного ряда  . Тогда
. Тогда является
является — решение дифференциального уравнения
— решение дифференциального уравнения  . Тогда
. Тогда решение
решение  является продолжением решения
является продолжением решения  . Тогда
. Тогда может быть продолжено
может быть продолжено — подмножество интервала сходимости. Тогда ряд сходится на множестве равномерно, если оно
— подмножество интервала сходимости. Тогда ряд сходится на множестве равномерно, если оно . Какие утверждения верны:
. Какие утверждения верны: верны:
верны:
